
Boa parte das imagens utilizadas neste site pertencem a terceiros, que gentilmente permitiram sua utilização, assim sendo não posso
autorizar a utilização das imagens deste site.
© CIÊNCIA-CULTURA.COM - Responsável - Ricardo Pante
EMÍLIO
GINO
SEGRÉ
nasceu
em
Tivoli,
Itália
em
1905.
Em
1959
ganhou
o
Prêmio
Nobel
de
Física
com
a
descoberta
do
antipróton.
Já
lecionou
nas
principais
universidades
dos
Estados
Unidos.
Suas
pesquisas
e
seus
trabalhos
mais
importantes
sempre
se
voltaram
para
a
antimatéria.
Neste
artigo
Segré
mostra
que
a
lógica
de
Einstein
é
irrefutável,
embora
na
época
dele
soasse
desagradável
para
muitos
físicos,
em
razão
de
sua
aparente
contradição com a experiência do cotidiano. Segré, na década de 60, contribuiu com muitos artigos de Física para a Enciclopédia Britânica.
Este artigo é da Revista Humanidades - Universidade de Brasília
Julho/setembro 1983 - número 4
Einstein
atacou
o
problema
da
transformação
do
tempo
e
do
espaço
com
enfoque
profundo
e
entusiasmo
quase
infantil.
Com
uma
lógica
convincente,
analisou
cuidadosamente
os
conceitos
de
tempo
e
espaço
usando
um
método
operacional,
que
para
cada
conceito
introduzido,
exigia
uma
especificação
rigorosa
e
concreta
de
como
medir
as
magnitudes
envolvidas.
Naturalmente
estava
interessado
não
nos
instrumentos
e
em
mecânica,
mas
na
lógica
da
experiência.
Resultados
inteiramente
inesperados
surgiram
de
sua
análise,
como,
por
exemplo,
a
relatividade
da
simultaneidade:
fatos
que
ocorrem
em
diferentes
locais
e
ao
mesmo
tempo
para
um
observador
não
parecem
simultâneos
para
outro
que
se
mova
em
relação
ao
primeiro.
Do
mesmo
modo,
há
o
paradoxo
dos
gêmeos:
um
irmão
gêmeo
permanece
em
um
sistema
de
referência
e
o
outro
se
afasta
em
movimento
uniforme
e
retilíneo,
inverte
a
direção
do
movimento
e
retorna.
Quando
o
segundo
irmão
gêmeo
volta
a
encontrar
o
primeiro,
acha-o
mais
velho.
Se
formos
céticos
a
esse
respeito,
a
experiência
já
foi
realizada
com
partículas
que
se
desintegram,
e
o
resultado
previsto
pela
relatividade
foi
confirmado.
Acima
de
tudo,
ficou
evidente
que
não
era
a
transformação
de
Galileu,
mas
a
de
Lorentz
que
correspondia
à
maneira
correta
de
medir
o tempo e o espaço.
A
lógica
de
Einstein
é
irrefutável,
embora
à
época
soasse
desagradável
a
muitos
físicos,
em
razão
de
sua
aparente
contradição
com
a
experiência do quotidiano. Sublinho aparente porque, na realidade, essa contradição não existe.
Um
dos
professores
de
Einstein,
Hermann
Minkowski
(1864-1909),
inventou
uma
delicada
expressão
matemática
para
a
transformação
das
coordenadas
de
espaço
e
tempo.
Introduziu
um
espaço
quadrimensional,
três
dimensões
de
espaço
e
uma
de
tempo.
A
característica
específica
desse
espaço
é
que
a
distância
entre
dois
pontos
não
é
dada
pelo
teorema
de
Pitágoras
que,
no
espaço
ordinário,
diz
espaço
que
s
2
=
x
2
+
y
2
+
z
2
.
O
espaço
quadrimensional
de
Minkowski
usa
uma
forma
um
pouco
diferente:
s
2
=
x
2
+
y
2
+
z
2
–
c
2
t
2
.
A
introdução
do
tempo
em
espaço
quadrimensional
e
o
sinal
menos
em
frente
ao
último
termo
é
que
modificam
radicalmente
a
situação.
Em
uma
conferência
histórica,
pronunciada
em
1908,
Minkowski
apresentou seus novos conceitos com as seguintes palavras:
"Cavalheiros,
as
noções
de
espaço
e
tempo
que
desejo
apresentar-lhes
emergiram
do
terreno
da
física
experimental
e
ali
reside
sua
força.
São
radicais.
Daqui
em
diante,
o
espaço
por
si
mesmo,
e
o
tempo,
por
si
mesmo,
estão
destinados
a
transformar-se
em
meras
sombras
e
apenas
uma
espécie
de
união
dos
dois
preservará
uma
realidade
independente".
(Conferência
aos
80.
Versammlung
Deutscher
Naturforscher
und
Aerzte, Colônia, 1908.)
Quando
Minkowski
viu
o
trabalho
original
de
Einstein,
lembrou-se
de
seu
aluno
e
disse
o
seguinte:
"Imaginem
só!
Eu
nunca
esperaria
uma coisa tão inteligente vinda desse camarada".
As
consequências
da
teoria
da
relatividade
são
vastas,
profundas
e
inesperadas.
Segundo
o
modo
de
pensar
de
Einstein,
a
velocidade
da
luz
aparece
como
uma
constante
universal
e
seu
caráter
fundamental
transcende
sua
conexão
histórica
com
o
eletromagnetismo.
Relaciona
espaço
e
tempo
na
transformação
de
Lorentz;
é
a
velocidade
limite
que
não
pode
ser
superada
na
transmissão
de
sinais;
aparece
na
conexão
entre
velocidade,
energia e momentum de um ponto material que tem a massa m em repouso. Essa conexão é dada pelas fórmulas
A
massa
dos
corpos,
definida
como
proporção
entre
força
e
aceleração,
torna-se
variável
com
a
velocidade.
A
conservação
da
massa
já
não
constitui
uma
lei
precisa
e
substitui
uma
generalização
da
conservação
da
energia,
na
qual
a
massa
pode transformar-se em energia segundo a fórmula
mc
2
= E
Físicos modernos chegaram a descobrir "partículas" sem massa sendo a
mais notável o quantum de luz. Para essas partículas, E = cp, e elas se movem com a
velocidade da luz em relação a qualquer sistema inercial.
Os
novos
conceitos
desnortearam
os
físicos.
Mesmo
um
grande
físico
teórico
como
H.A.
Lorentz,
que
achara
a
transformação
básica
para
a
relatividade,
teve
dificuldade
para
aceitar
as
novas
ideias.
Não
que
a
matemática
apresentasse
um
obstáculo:
as
dificuldades
nesse
campo
eram
mínimas.
A
barreira
estava
na
verdadeira
forma
de
pensar
e,
em
consequência,
a
teoria
só
veio
a
tornar-se
familiar
para
os
físicos
uma
geração
mais
tarde.
Ideias
genuinamente
novas
em
físicas
solidificam-se
com
muita
lentidão,
sobretudo
porque
a
geração
que
as
cria
não
consegue
"senti-las".
Os
físicos
mais
amadurecidos
podem
aprender,
mas
a
verdadeira
assimilação
ocorre
quando
os
contemporâneos
morrem
e
os
sucessores
passam
a
considerar
as
ideias
novas
como
básicas.
Testemunhei
esse
fenômeno
bem
de
perto
na
mecânica
dos
quanta.
Devo
acrescentar
ainda
que
a
nova
geração,
doutrinada
desde
o
início,
não
tem
consciência
de
muitos
dos
dilemas
e
objeções
que
os criadores têm de enfrentar.
A
relatividade
só
foi
sendo
aceita
aos
poucos.
Por
exemplo,
mesmo
em
1922, a Academia Sueca concedeu o Prêmio Nobel a Einstein "pelo serviço por ele
prestado
à
física
teórica
e
particularmente
por
sua
descoberta
da
lei
do
efeito
fotoelétrico".
Pode
parecer
estranho
que
a
relatividade
não
seja
mencionada,
mas,
numa
retrospectiva,
a
meu
ver,
houve
sabedoria
nessa
escolha.
Não
é
que
a
relatividade
seja
um
tema
de
importância
secundária,
mas é que os outros "serviços" de Einstein foram imensos.
Voltemos
agora
ao
primeiro
dos
dois
documentos
escritos
por
Einstein
no
surpreendente
ano
de
1905.
A
meu
ver,
é
uma
das
maiores
obras
já
realizadas
em
física.
Naquela
época,
os
cientistas
sabiam
que
a
luz
era
constituída
de
ondas
eletromagnéticas;
se
havia
alguma
coisa
de
certo,
era
isso.
No
entanto,
Einstein
tinha
dúvidas
e
revelou
a
natureza
dual
da
luz
—
corpuscular
e
ondulatória.
Essa
descoberta,
junto
com
o
aspecto
dual
correspondente
da
matéria,
tornou-se
a
maior
conquista
do
século.
Newton
e
Huygens
foram
inesperadamente
reconciliados
por
uma
profunda
revolução na filosofia natural, que mostrou estarem ambos, em parte, certos.
Planck
quantizava
a
energia
dos
osciladores
que
formavam
as
paredes
de
sua
versão
do
corpo-negro.
Com
referência
à
radiação
propriamente
dita,
pôde
apenas
dar
a
expressão
u
(v,
t).
Acredito
que
ele
mesmo
não
tinha
dúvidas
de
que
as
equações
de
Maxwell
descreviam
exatamente
as
ondas
eletromagnéticas
que
enchem
a
cavidade.
Einstein,
no
entanto,
perguntava-se
se
a
descrição
de
Maxwell
era
compatível
com
a
fórmula
do
corpo-
negro
de
Planck
e
chegou
à
surpreendente
conclusão
de
que
a
própria
luz
devia
ser
composta
de
quanta
quase-corpusculares.
Não
posso
deixar
de
lado seu raciocínio porque, quando o li, sua força e simplicidade praticamente me arrasaram quase que fisicamente.
Einstein
observou
que
a
derivação
de
Planck,
ao
considerar
as
trocas
de
energia
entre
osciladores
e
radiações,
pressupõe
implicitamente
que
a
energia
pode
ser
absorvida
e
emitida
pelo
oscilador
isolado
apenas
em
quanta
de
magnitude
hv,
isto
é,
que
a
energia
de
uma
estrutura
mecânica
capaz
de
oscilações,
bem
como
a
energia
da
radiação,
pode
ser
transferida
apenas
nesses
quanta,
em
contradição
com
as
leis
da
mecânica
e
da
eletrodinâmica".
A
física
clássica
leva-nos
inevitavelmente
ao
enfoque
Rayleigh-Jeans
da
fórmula
de
Planck.
É
válido
para
hv/kt
<<
1,
e
nela
h
não
aparece.
Para
hv/kt
>>
1,
a
fórmula
de
Wien
é
válida,
e
os
conceitos
clássicos
fracassam.
Einstein
concentrou
sua
atenção
na
fórmula
de
Wien
e
a
partir
dela
obteve
uma
expressão para a entropia de uma radiação de certa frequência contida em certo volume, ou, mais precisamente,
para
a
variação
dessa
entropia
ao
mudar
o
volume,
mantendo
constante
a
energia.
Observa
ele
que
"essa
equação
mostra
que
a
entropia
da
radiação
monocromática
de
densidade
suficientemente
pequena
varia
com
o
volume
como
a
entropia
de
um
gás
ideal...”
Depois
vai
adiante,
para
calcular
a
entropia pelo método de Boltzmann, concluindo que:
"Se
a
radiação
monocromática
de
frequência
v
e
energia
E
é
encerrada
em
um
volume
v
por
paredes
perfeitamente
refletoras,
então
a
probabilidade (relativa) de que a qualquer momento toda a energia de radiação seja encontrada no volume parcial
n
do volume
n
0
é dada por
A partir daí, concluímos ainda que a radiação monocromática de pequena densidade de energia (dentro do campo de validade da
fórmula de radiação de Wien) comporta-se, em relações termodinâmicas teóricas, como se consistisse de quanta distintos de energia independentes
de magnitude hv. *
* Para facilitar ao leitor moderno, usei as constantes h e k. Einstein usa B = h/k e RN = k sendo R a constante dos gases e N o número de Avogadro.
Einstein
leva
esse
resultado
muito
a
sério,
a
despeito
da
prova
esmagadora
de
todos
os
fenômenos
de
propagação
em
favor
de
uma teoria de ondas para a luz, e diz o seguinte:
"Se
então,
na
medida
da
dependência
da
entropia
no
volume,
a
radiação
monocromática
de
densidade
suficientemente
pequena
se
comporta
como
um
meio
descontínuo
consistindo
de
quanta
de
energia
de
magnitude
hv,
é
razoável
indagar-se
se
as
leis
de
emissão
e
transformação da luz são constituídas como se a luz fosse composta desses mesmos quanta de energia.”
Trataremos desse assunto no próximo capítulo". (Einstein, Annalen der Physik, 19, 143, (1904).)
No
capítulo
seguinte,
ele
trata
do
efeito
fotoelétrico
bem
como
de
análises
fotoquímicas
e
outras
ideias.
Tudo
isso
são
exemplos
que
confirmam sua hipótese dos quanta de luz.
Foi
enorme
o
progresso
realizado
a
partir
das
ideias
de
Planck.
Planck
tinha
apenas
quantizado
os
osciladores
materiais
formando
as
paredes
do
corpo-negro,
talvez
sem
mesmo
acreditar
na
realidade
de
níveis
de
energia.
O
tônus
do
trabalho
inicial
de
Planck
—
e
mesmo
do
trabalho
posterior
—
dá
a
impressão
de
que
a
quantização
era
para
ele
pouco
mais
que
um
artificio
de
cálculo.
Para
Einstein,
por
outro
lado,
era
um
fenômeno
fundamental;
em
particular,
a
luz,
isto
é,
o
próprio
campo
eletromagnético,
é
quantizado.
Naturalmente
a
quantização
apresenta
enormes
dificuldades
se
se
tentar
conciliá-la
com
fenômenos
de
propagação
da
luz.
Em
vez
de
fugir
desses
problemas,
Einstein
reconheceu
sua
natureza
fundamental e nunca deixou de meditar sobre eles até que fossem encontradas as soluções, em parte por ele mesmo, em parte por outros físicos.
Agora
voltemo-nos
para
o
segundo
dos
estudos
de
Einstein
de
1905.
No
ano
de
1827,
o
botânico
escocês
Robert
Brown
(1773-1858)
observou
que
grãos
de
pólen
ou
outros
objetos
pequenos
suspensos
na
água
fazem
um
movimento
aleatório.
Esse
movimento,
chamado
de
browniano,
se
deve
ao
impacto
das
moléculas
do
fluido
que
cercam
o
objeto.
Einstein
apresenta
uma
teoria
sobre
o
movimento
browniano,
com
base
na
teoria
cinética
dos
gases.
Essa
teoria
dá
um
método
novo
e
direto
para
determinar
a
constante
de
Boltzmann
e,
por
conseguinte,
o
número
de
Avogadro, e uma prova quase tangível da existência de moléculas.
Esses
trabalhos
extraordinários
foram
notados
pela
comunidade
científica:
já
em
março
de
1906,
Planck
publicou
um
estudo
de
Einstein
sobre
a
teoria
da
relatividade.
Mas
ninguém
tinha
visto
o
autor.
Nem
o
autor
havia
deixado
o
escritório
de
patentes
para
conversar
com
os
grandes
físicos
teóricos.
Não
obstante,
alguns
jovens
e
ousados
cientistas
decidiram
ir
a
Berna
para
saber
quem
era
aquele
Senhor
Albert
Einstein.
Encontraram-no
em
seu
escritório.
Sua
vida
particular
parecia
um
tanto
boêmia,
mas
ele
era
polido
e
prontificou-se
a
esclarecer
quaisquer
dúvidas
que
existissem
a
respeito
de
suas
ideias.
Einstein
começou
a
corresponder-se
com
Planck
e
Lorentz
e
logo
as
autoridades
suíças
ofereceram-lhe
um
modesto
cargo
na
Universidade
de
Berna.
De
início,
não
quiseram
nomeá-lo
Privat
Dozent
por
questões
burocráticas,
mas
em
1908
a
Universidade
de
Zurique
concedeu-lhe
tal
título.
A
Universidade
Alemã
de
Praga
ofereceu-lhe
uma
cátedra
em
1909
e
ele
a
aceitou.
Mas
Einstein
não
se
sentia
feliz
em
Praga,
na
Áustria
dos
Habsburgos,
onde
predominava
uma
atmosfera
hipócrita
e
antissemita.
Einstein
não
tinha
muita
simpatia
pela
religião
em
termos
formais
e
era
fundamentalmente
agnóstico,
pelo
menos
no
que
diz
respeito
a
qualquer
teologia
formal.
Ficou
aliviado
quando,
em
1912,
pôde
retornar à sua amada Suíça, desta vez para a Escola Politécnica de Zurique, onde havia estudado.
Em
Praga,
Einstein
fizera
amizade
com
P.
Ehrenfest,
amizade
que
mais
tarde
veio
a
fortalecer-se
e
durou
até
a
morte
de
Ehrenfest.
Paul
Ehrenfest
(1880-1933)
era
um
físico
teórico
austríaco
que
tinha
sido
aluno
de
Boltzmann.
Casara-se
com
uma
física
russa,
Tatiana,
e
com
ela
escreveu um famoso artigo sobre mecânica estatística para a Encyclopedia of Mathematics. Ehrenfest possuía mais capacidade para esclarecer pontos
obscuros
da
física
do
que
para
criar
teorias
originais.
Era
um
professor
de
alta
capacidade
didática
e
demonstrava
muita
diligência
nas
tentativas
de
identificar
novos
talentos.
Era
famoso
pelo
afeto
com
quem
encorajava
os
jovens
e
estimado
e
estimado
por
seus
muitos
amigos
e
alunos,
em
razão
de
suas
qualidades
humanas.
Sucedeu
a
Lorentz
em
1912
e
fundou
uma
escola
que
logo
começou
a
ampliar-se.
Infelizmente,
Ehrenfest
era
sujeito
a
fases de profunda depressão e, durante uma delas, em 1933, suicidou-se.
Um
estudante
de
físico-química
originário
de
rica
família
de
Praga
uniu-se
a
Einstein.
Tratava-se
de
Otto
Stern
(1888-1969).
Stern
havia-se
dado
conta
de
que
Einstein
era
o
físico
do
futuro,
ou
melhor,
do
presente,
e
aproveitou-se
de
sua
própria
independência
financeira
para
estudar e trabalhar com ele. Este é outro exemplo do inter-relacionamento das carreiras de muitos dos grandes físicos.
Por
essa
época,
Einstein
já
se
tinha
tornado
um
físico
importante
do
ponto
de
vista
profissional.
Em
1909,
em
uma
reunião
realizada
em
Salzburg,
conheceu
Planck,
Wien,
Sommerfeld,
Rubens,
Nernst
e
outros
grandes
físicos
modernos.
Sentiu
prazer
em
debater
frente
a
frente
com
todos eles. Antes disso, porém, já havia aperfeiçoado suas ideias de 1905.
Conforme
mencionei
acima,
ao
calcular
a
entropia
da
radiação
e
adotar
a
lei
de
Wien
para
u(v,T),
Einstein
concebera
a
ideia
dos
quanta
de
luz
e
relacionara-a
com
provas
experimentais.
A
entropia
da
radiação
está
intimamente
vinculada
à
flutuação
da
energia
contida
em
um
determinado
volume
e
a
hipótese
dos
quanta
de
luz
fornece
uma
expressão
bastante
simples
para
tais
flutuações.
O
que
acontece
se
se
efetuam
os
cálculos,
usando,
não
a
lei
aproximada
de
Wien,
que
só
é
válida
se
hV
>>>kT,
mas
a
lei
exata
de
Planck?
Einstein
fez
o
cálculo
mais
uma
vez
e
conseguiu uma fórmula notável para a flutuação da energia contida em um volume fixo e em certo intervalo de frequência em torno de V.
Einstein
achou
dois
termos
que
tinham
de
ser
somados.
O
primeiro
é
um
termo
obtido
em
1905
com
a
fórmula
de
Wien
e
é
perfeitamente
análogo
à
expressão
da
flutuação
do
número
de
moléculas
gasosas
em
um
volume.
Indica
a
estrutura
granular
da
energia
radiante
e
confirma
que
E
=
nhV,
isto
é,
que
a
luz
se
comporta
como
se
fosse
composta
de
quanta
de
energia
E
=
h
V
.
A
segunda
expressão,
por
outro
lado,
é
exatamente
a
que
se
obteria
a
partir
da
teoria
eletromagnética
pura
e
é
causada
pela
interferência
construtiva
ou
destrutiva
das
ondas.
O
fato,
digno
de
nota,
da
presença
de
ambos,
indica
a
natureza
dual
da
luz
—
ondulatória
e
corpuscular.
As
ideias
de
Newton
e
de
Huygens,
que
pareciam
exclusivas entre si, são confirmadas. Conforme Einstein escreveu em 1909:
"É
inegável
que
existe
um
extenso
grupo
de
dados,
relacionados
à
radiação,
que
mostram
ter
a
luz
certas
propriedades
fundamentais
que
podem
ser
entendidas
muito
mais
facilmente
a
partir
do
ponto
de
vista
da
teoria
newtoniana
de
emissão
do
que
a
partir
do
ponto
de
vista
da
teoria
ondulatória.
Portanto,
sou
de
opinião
que
a
próxima
fase
do
desenvolvimento
da
física
teórica
nos
trará
uma
teoria
da
luz
que
pode
ser
interpretada como uma espécie de fusão das teorias ondulatória e da emissão..."
Enquanto
isso,
em
1907,
Einstein
havia
descoberto
outra
importante
aplicação
das
ideias
do
quantum.
Em
1819,
P.L.
Dulong
e
A.
T.
Petit
tinham
anunciado
que,
segundo
seus
cálculos,
"Les
atomes
de
tous
les
corps
simples
ont
exactement
Ia
même
capacité
pour
Ia
chaleur"
("Os
átomos
de
todos
os
elementos
têm
exatamente
a
mesma
capacidade
térmica"),
e
Boltzmann
tinha
explicado
esse
fato
com
o
princípio
da
equipartição
da
energia.
No
entanto,
quando
se
tornou
possível
medir
calores
específicos
a
baixas
temperaturas,
graças
à
disponibilidade
de
ar
líquido
e
a
outros
métodos
criogênicos,
descobriu-se
que
a
lei
de
Dulong
e
Petit
tinha
muitas
exceções.
Einstein
forneceu
a
razão
para
a
dependência
de
temperatura
do
calor
específico
representando
átomos
em
cristais
como
osciladores
de
determinada
frequência.
Segundo
a
teoria
dos
quanta,
eles
só
poderiam
ter
a
energia
nhv
com
n
como
número
inteiro.
Se
hv<<
kT,
estaremos
no
domínio
da
física
clássica
e
os
osciladores
terão
a
energia
média
de
3kT.
O
calor
atômico,
isto
é,
o
calor
específico
referente
a
um
átomo,
é
3k,
conforme
Dulong
e
Petit
haviam
achado.
Se,
entretanto,
kT
<<hv,
a
quantização
torna-se
apreciável
e
obteremos
um
calor
específico
muito
diferente
do
clássico.
Do
ponto
de
vista
qualitativo,
quando
os
osciladores
são
altamente
estimulados,
a
adição
de
um
quantum
de
energia
produz
uma
mudança
energética
que
é
pequena
em
comparação
à
energia
já
existente
no
oscilador
e
aí
não
estaremos
muito
longe
do
caso
clássico,
que
pressupõe
que
a
energia
muda
continuamente.
Para
que
tal
situação
ocorra,
a
temperatura
do
ambiente
em
volta
do
oscilador
deve
ser
tal,
que
kT
>>
hv.
Na
realidade,
a
energia
do
oscilador
será
então
kT
em
termos
brutos,
o
que
é
muito,
se
comparado
com
os
possíveis
saltos
de
energia
hV.
No
caso
extremo
e
oposto
kT
<<
hv,
a
agitação
da
temperatura
é
insuficiente
para
produzir
saltos
de
quanta
no
oscilador,
que,
assim,
se
torna
incapaz
de
absorver
energia
do
ambiente
em
torno.
O
comportamento
do oscilador é dominado por suas propriedades quânticas e o calor específico desaparece.
A teoria foi aperfeiçoada por P. Debye e outros e está em consonância com dados experimentais.
Tais
considerações
são
importantes
porque
mostram
que
a
constante
h
desempenha
um
papel
vital
na
mecânica
das
moléculas
e
dos
átomos.
O
êxito
desses
conceitos
serviu
para
despertar
mais
interesse
ainda
pelas
conceituações
quânticas,
que
ainda
se
restringiam
a
um
círculo
muito reduzido de iniciados.
Em
1911,
realizou-se
a
primeira
série
de
Conferências
Solvay
sobre
radiação
e
quanta.
Essas
conferências
derivam
seu
nome
de
Ernst
Solvay,
o
inventor
de
um
método
industrial
para
a
preparação
de
carbonato
de
sódio,
ou
soda.
Solvay
instituiu
e
financiou
uma
série
de
encontros
internacionais
sobre
física,
com
temas
preestabelecidos,
para
os
quais
se
convidavam
os
grandes
físicos
relacionados
à
área
escolhida.
As
conferências,
limitadas
a
cerca
de
trinta
pessoas,
tinham
lugar
em
Bruxelas.
A
orientação
dos
debates
e
a
relação
de
convidados
para
o
primeiro
deles
eram
elaboradas
em
grande
parte
por
H.
Walther
Nernst
1864-1941
professor
de
físico-química
em
Berlim,
um
dos
principais
termodinamicistas
da
época
e
uma
força
da
ciência
alemã.
Nernst
havia
descoberto
um
teorema
importante
às
vezes
chamado
de
terceiro
princípio
da
termodinâmica,
segundo o qual a entropia de qualquer substância pura ao zero absoluto era a mesma: Zero.
Seu
teorema
tinha
profundas
raízes
na
teoria
quântica.
Em
razão
de
suas
altas
qualificações
em
física
e
linguística
e
de
suas
habilidades
diplomáticas
e
presságio
geral,
H.A.
Lorentz
era
um
convidado
permanente
e
quase
sempre
atuava
como
presidente
do
encontro.
O
número
restrito
de
participantes
e
o
nível
dos
convidados
asseguravam
debates
acalorados
e
profícuos.
Por
tradição,
os
soberanos
belgas
mostravam
seu
interesse
pelas
reuniões
convidando
os
participantes
a
um
jantar.
Como
resultado
desses
encontros,
Einstein
tomou-se
amigo
da
Rainha
Elizabeth
da
Bélgica
e
com ela manteve uma correspondência que durou muitos anos.
Na
conferência
de
1911,
Planck,
como
sempre,
manifestou
um
ponto
de
vista
conservador
e
prudente,
enquanto
Einstein,
que
estava-se
tornando
conhecido
como
a
figura
de
maior
realce,
mostrou-se
mais
flexível.
Pouco
depois,
quando
Einstein
recebeu
a
proposta
de
uma
cátedra
na
Escola
Politécnica
de
Zurique,
Marie
Curie
e
Poincaré,
que
o
haviam
conhecido
na
reunião
de
Solvay,
expressaram
abertamente,
em
uma
carta
de
recomendação, o alto conceito que por ele tinham.
Einstein
foi
para
a
Escola
Politécnica
em
1912,
mas
ali
ficou
pouco
tempo.
Os
grandes
físicos
de
Berlim
o
queriam
na
capital
do
Reich
e
assim
apresentaram-lhe
ofertas
bastante
atrativas
para
o
Kaiser
Wilhelm
Institute
ou
para
a
Academia
Prussiana,
à
sua
livre
escolha.
As
funções
de
magistério
seriam
mínimas
e
ele
teria
a
máxima
liberdade
para
trabalhar,
um
salário
generoso
e
outras
vantagens.
Nernst
e
Planck
foram
a
Zurique
para
apresentar
a
oferta
pessoalmente,
o
que
constituiu
uma
atitude
rara.
Einstein
não
precisou
de
mais
que
um
dia
para
decidir-se.
Informou
aos
visitantes
que
daria
um
passeio
e
retornaria
com
uma
rosa—
uma
rosa
vermelha
se
aceitasse
ou
uma
rosa
branca
se
recusasse.
Retornou
com
uma
rosa
vermelha.
Mas
insistiu
em
uma
condição:
queria
manter
a
cidadania
suíça.
Essa
insistência
provocou
alguns
problemas,
pois,
embora
Einstein
se
considerasse cidadão suíço, a Prússia o considerava cidadão prussiano.
A
despeito
de
sua
brilhante
posição,
Einstein
não
se
sentia
bem
na
Alemanha
imperial.
Apreciava
a
companhia
dos
colegas
e
outras
atrações
oferecidas
por
Berlim,
mas
não
o
militarismo
prussiano.
Para
escapar
à
atmosfera
de
quartel
que
sentia
em
Berlim,
quase
sempre
ia
até
a
Holanda,
para
encontrar-se
com
os
amigos
Lorentz
e
Ehrenfest.
No
início
de
sua
estada
na
Alemanha,
Einstein
divorciou-se;
mais
tarde,
veio
a
casar-se com uma prima, com quem viveu o resto de sua vida.
Estamo-nos
aproximando
do
fatal
agosto
de
1914.
Einstein
estava
engajado
nas
primeiras
pesquisas
sobre
a
relatividade
geral,
uma
ampla
extensão
do
princípio
da
relatividade
para
movimentos
arbitrários.
É
claro
que
dois
sistemas,
acelerados
um
em
comparação
com
o
outro,
não
são
equivalentes.
O
fato
é
que
aparecem
forças
inerciais
em
um
que
não
são
encontradas
no
outro.
Um
exemplo
simples
é
um
elevador
em
queda
livre
sobre
a
superfície
da
terra:
para
um
observador
que
esteja
dentro
dele,
a
gravidade
desaparece.
Tal
fato
obviamente
não
é
a
mesma
coisa
que
um
elevador
em
repouso
em
relação
à
terra,
para
o
qual
a
gravidade
efetivamente
existe.
Einstein,
no
entanto,
observou
que,
ao
introduzirem-se
campos
gravitacionais
apropriados,
podem-se
tornar
os
dois
sistemas
acelerados
equivalentes
um
ao
outro.
Para
que
isso
seja
possível,
é
necessário
que
as
massas
inerciais
que
aparecem
na
equação
F
=
ma
sejam
iguais
à
massa
gravitacional
que
aparece
na
F
=
kmm'/r2.
Esse
fato,
digno
de
nota,
quase
sempre
expresso
quando
se
diz
ser
a
massa
gravitacional
igual
à
massa
inercial,
tinha
sido
descoberto
por
Galileu
em
suas
experiências
quase
lendárias
na
torre
inclinada
de
Pisa
e
confirmado
por
Newton,
que
cuidadosamente
constatou
que
pêndulos
do
mesmo
comprimento,
mas
de
materiais
diferentes,
têm
o
mesmo
período.
Com
maior
precisão,
o
Barão
R.
von
Eõtvõs
confirmou
esse
fato
na
Hungria,
em
1891,
e
precisão
ainda
maior foi conseguida por R.H. Dicke em 1936.
A
relatividade
geral,
em
oposição
à
relatividade
restrita,
não
estava
na
primeira
linha
do
interesse
dos
físicos,
e
Einstein
teve
de
enfrentar
sozinho
o
problema.
Do
ponto
de
vista
matemático,
a
teoria
geral
é
consideravelmente
mais
difícil
do
que
a
teoria
específica
da
relatividade
e
exige
o
uso
de
"análise
tensorial",
que,
na
época,
era
praticamente
desconhecida
dos
físicos.
O
próprio
Einstein
sentiu-se
impedido
pelas
dificuldades
matemáticas,
até
que
seu
amigo
Grossmann
lhe
apresentou
as
obras
de
B.
Riemann
e
B.
Christoffel
e,
mais
importante,
as
de
G.
Ricci-Curbastro
e
T.
Levi-Civita,
que
forneceram
os
necessários
instrumentos
matemáticos.
Einstein
pôde
então
operar
em
espaços
curvos
e
relacionar
os
efeitos
gravitacionais à curvatura do espaço que, por sua vez, é relacionada à presença de matéria ou energia.
Estou-me
antecipando
um
pouco.
A
declaração
de
guerra
em
1914
foi
acompanhada
de
uma
investida
geral
de
patriotismo
ingênuo
e
primário,
especialmente
na
Alemanha.
Reagindo
às
acusações
lançadas
pelos
Aliados,
talvez
às
vezes
exageradas,
contra
a
Alemanha,
principalmente
no
que
diz
respeito
à
invasão
da
Bélgica
neutra,
os
cientistas
alemães
responderam
com
um
manifesto
defensivo
em
que
cada
frase
começava
com
a
expressão:
"Es
ist
nicht
wahr.
..
(Não
é
verdade...)
e,
ao
final,
proclamava
a
solidariedade
dos
cientistas
com
os
militares.
Infelizmente,
entre
os
signatários
do
manifesto
estavam
nomes
altamente
respeitáveis,
como
Roentgen,
Planck,
Nernst,
Wien
e
muitos
outros.
Quando
se
dava
o
caso,
eles
acrescentavam
títulos
aos
nomes,
como
Geheimrat
(Conselheiro
Privado
do
Imperador)
ou
Excellenz
(Sua
Excelência),
detalhe
aliás
bastante
irônico,
se
pensarmos
que
alguém
como
Roentgen
poderia
imaginar
que
um
título
oficial
iria
acrescentar
força
à
sua
assinatura.
Mas
era
assim
a
Alemanha
imperial.
É
evidente
que
muitos
dos
signatários,
inclusive
Roentgen,
eram
ingênuos
e
mais
tarde
se
arrependeram
dessa
atitude.
Outros,
como
Planck,
aprenderam
a
lição
com
os
próprios
fatos.
Embora
continuassem
arraigadamente
patriotas,
não
foram
envolvidos
tempos
depois
pela
retórica
nacionalista
de
Hitler.
Einstein
recusou-se
a
assinar
o
documento
e
chegou
a
pensar
em
organizar
um
manifesto
de
oposição,
mas
não
levou
o
plano
adiante. De qualquer modo, já havia feito sérios inimigos em virtude de sua oposição política.
Einstein
estava
absorvido
em
seus
esforços
no
sentido
de
desenvolver
a
relatividade
geral.
Várias
vezes
julgou
ter
atingido
a
meta
tão
almejada,
logo
descobrindo
que
havia
falhas
graves
nessa
teoria.
Finalmente,
conseguiu
cumprir
seu
programa
de
formulação
de
leis
físicas
de
uma
maneira
válida
para
qualquer
sistema
de
referências,
provocando
uma
nova
interpretação
da
gravitação.
O
progresso
conceitual
e
a
clareza
da
teoria
são
marcantes,
embora
os
resultados
experimentais
sejam
modestos.
Previa
ela
alguns
pequenos
efeitos
que
podiam
fornecer
provas
experimentais:
a
mudança
do
periélio
de
Mercúrio;
o
desvio
de
raios
de
luz
por
uma
massa,
efeito
visível
em
um
eclipse
solar;
e
a
mudança
de
frequência
das
linhas
espectrais
emitidas
por
astros
maciços.
Infelizmente,
todos
esses
efeitos
são
pequenos
e
de
difícil
observação,
de
modo
que,
mesmo
agora,
não
há
nenhuma
confirmação
experimental
absoluta
ou
inequívoca
da
teoria
geral
da
relatividade.
Não
obstante,
a
redução
da
relatividade
a
um
efeito
geométrico
da
curvatura
do
espaço
é
um
conceito
magnífico
e
de
imensa
importância
em
astrofísica
e
cosmologia.
É
aqui
que
a relatividade geral recebe a parte que lhe cabe e se torna indispensável para descrever e interpretar as observações astronômicas.
Em
1917,
Einstein
publicou
outra
obra
de
grande
importância,
uma
nova
e
bem
simples
derivação
da
lei
do
corpo-negro,
que
dá
continuidade
a
conceitos
bastante
profundos.
A
emissão
de
luz
já
não
era
considerada
de
um
ponto
de
vista
maxwelliano.
Pela
primeira
vez,
leis
estatísticas, as mesmas que se aplicam ao decaimento radioativo, eram estendidas a fenômenos eletromagnéticos.
A
teoria
atômica
de
Bohr
já
existia
então,
mas
o
mecanismo
da
emissão
da
luz
a
partir
de
um
átomo
continuava
a
ser
um
mistério.
Einstein
conseguiu
levantar
uma
ponta
da
cortina
que
encobria
o
fenômeno
e
seus
documentos
de
1917
eram
muito
perspicazes
e
assinalaram
um
marco
na
teoria
moderna.
Neles,
abandonou
a
causalidade
estrita
da
física
clássica
e
apresentou
conceitos
de
probabilidade.
Nessas
condições,
seu
trabalho
continha
o
germe
da
mecânica
quântica
e
da
profunda
revolução
por
ela
causada.
Além
do
mais,
sem
qualquer
menção
explícita
das
aplicações, continha também as ideais básicas ao funcionamento dos lasers e maser tão empregados hoje em dia.
Também
neste
caso
a
ideia
profunda
de
Einstein
é
tão
simples,
que
pode
ser
explicitada
em
palavras,
sem
ser
necessário
recorrer
a
fórmulas.
Einstein
examinou
um
corpo-negro
em
equilíbrio
térmico
contendo,
além
da
radiação,
átomos
especificamente
simples
com
apenas
dois
níveis
de
energia.
Um
pode
passar
de
um
nível
para
o
outro
emitindo
ou
absorvendo
um
quantum
de
luz
de
frequência
v
=
(E1
-
E2)h,
onde
E1
e
E2
são
as
energias
dos
dois
níveis.
Ao
precisar
que
o
átomo
e
a
radiação
se
mantêm
em
equilíbrio
estatístico,
isto
é,
que
o
número
de
átomos
que
passam
por
segundo
do
estágio
inferior
para
o
estágio
superior,
ou
vice-versa,
é
o
mesmo,
obteve
ele
notáveis
relações
entre
as
probabilidades
de
transição
e
a
emissividade
da
radiação.
Baseou
o
cálculo
na
probabilidade
de
ocorrência
do
decaimento
radioativo,
adequadamente
modificada.
Trata-se
de
um
enfoque
radicalmente
distinto
do
método
eletromagnético
clássico.
Einstein
chamou
de
A
a
taxa
de
transferência
espontânea
do
átomo
do
nível
superior
para
o
inferior,
e
de
B
a
taxa
de
transferência
do
estágio
superior
para
o
inferior,
ou
vice-versa,
sob
a
influência
da
radiação
de
emissividade
u
(v,
T).
Entre
outras
coisas,
mostrou
que
as
duas
taxas
de
transferência
induzida
são
iguais.
O
A
e
o
B
de
Einstein
atualmente
constituem um conceito básico em física.
A
introdução
dos
coeficientes
A
e
B
com
seu
significado
baseado
na
probabilidade,
em
conexão
com
a
emissão
de
luz,
representa
uma
tendência inteiramente nova e um prenúncio de coisas que estavam para acontecer.
Nesse
mesmo
documento
de
1917,
Einstein
forneceu
também
uma
nova
prova
do
resultado
que
havia
conseguido
anos
antes,
o
qual
dizia
que,
além
da
energia
hv,
os
quanta
de
luz
também
têm
uma
quantidade
de
movimento
hv/c
no
sentido
da
propagação
da
luz.
De
um
modo
notável,
chegara
ele
a
essa
conclusão,
que
deriva
diretamente
da
relatividade,
mediante
análises
sutis
—
e
até
certo
ponto
recônditas
—
das
flutuações da energia e da densidade do momentum (quantidade de movimento).
Enquanto
Einstein
estava
absorvido
nesses
estudos,
a
guerra
havia
tomado
seu
curso,
terminando
em
1918
com
a
derrota
da
Alemanha
e
a
ruína
do
velho
regime
do
Kaiser,
sem
nenhuma
lamentação
por
parte
de
Einstein.
Após
um
período
revolucionário,
a
nova
República
de
Weimar
trouxe
para
a
Alemanha
grandes
esperanças
de
democratização.
Mas
o
governo
mostrava-se
extremamente
fraco,
era
solapado
por
dentro
e
por
fora
e incapaz de governar com o vigor necessário.
Em
1919,
ocorreu
um
eclipse
total
do
sol,
que
possibilitou
a
constatação
de
algumas
das
consequências
da
relatividade
geral.
Realizaram-
se
várias
expedições
com
esse
propósito
e
os
resultados,
embora
não
muito
claros,
favoreceram
as
teorias
de
Einstein.
Nesse
ponto
é
que
a
popularidade
de
Einstein
eclodiu.
Por
motivos
que
não
são
para
mim
muito
claros,
ele
repentinamente
se
tornou
uma
figura
bastante
popular,
mesmo
entre
pessoas
que
nada
conheciam
de
sua
obra.
Era
tratado
como
um
astro
de
cinema
ou
como
um
grande
animador
de
auditório,
mas
também
passou
a
ter
inimigos
figadais,
sem
qualquer
motivo
racional.
Surgiu
até
mesmo
uma
sociedade
científica
ante
einsteiniana,
onde
nomes
respeitados
e
respeitáveis
se
misturavam
a
demagogos,
dementes
e
futuros
recrutas
nazistas.
Einstein
era
convidado
a
fazer
palestras
em
público
sobre
a
relatividade.
Aceitava
tais
convites,
mas
as
palestras
eram
interrompidas
por
seus
adversários
e
transformadas
em
torpes
demonstrações
políticas.
Einstein
não
tinha
muito
autocontrole
e
reagia
através
da
imprensa
de
uma
maneira
que,
segundo
seus
amigos
mais
íntimos,
não
era
absolutamente a ideal.
A
situação
tomou
um
rumo
difícil,
pois
os
extremistas
não
hesitavam
em
assassinar
os
inimigos.
O
assassinato
de
W.
Rathenau,
Ministro
dos
Negócios
Estrangeiros
da
República
de
Weimar,
foi
uma
advertência
a
respeito
do
que
poderia
acontecer.
Tratava-se
de
um
grande
patriota
e
figura
ilustre
da
indústria
alemã
que
trabalhara
infatigável
e
proveitosamente
em
favor
da
organização
da
economia
de
guerra
e
depois
fora
elevado
ao
cargo
de
Ministro.
Era
amigo
pessoal
de
Einstein
e
sua
morte,
bem
como
a
dos
socialistas
K.
Liebknecht
e
Rosa
Luxemburgo,
e
de
outras
figuras
notáveis, era apenas o prelúdio do que viria a acontecer durante a era nazista.
Einstein
já
estava
se
sentindo
saturado
e
iniciou
uma
longa
viagem
pelo
mundo.
Os
amigos
Planck,
von
Laue
e
outros,
insistiam
em
que
ele
não
deveria
abandonar
a
Alemanha
num
período
difícil
como
aquele
e
em
que
não
deveria
aceitar
nenhuma
das
inúmeras
propostas
que
vinha
recebendo
do
exterior.
Leyden
atraía-o
de
maneira
bastante
peculiar
tanto
por
causa
de
sua
amizade
com
Ehrenfest
quanto
por
causa
da
insistência
de
Lorentz
em
que
ele
ali
se
fixasse.
Mas,
ao
final
da
viagem,
Einstein
voltou
a
Berlim
depois
de
ter
estabelecido
relações
pessoais
nos
Estados
Unidos
e
em
outros
países.
A
situação
parecia
ter-se
acalmado
um
pouco
por
volta
de
1924,
e
ele
passou
a
levar
uma
vida
social
relativamente
ativa.
Em
casa,
recebia
grande
variedade
de
pessoas,
inclusive
o
pintor
Sleevogt,
o
médico
Plesch,
o
químico
P.
Haber,
os
músicos
F.
Kresiler
e
A.
Schnabel,
o
industrial
e
Ministro
do
Exterior
Graf
Rantzrau
e
o
pintor
M.
Liebermann.
Em
seus
momentos
de
lazer,
continuava
a
tocar
violino,
atividade
que
exerceu
durante
toda
a
vida.
Não
se
opunha
a
representar
o
papel
do
grande
cientista
e
era
evidente
que
gostava
disso.
Talvez
esse
fato
explique
algumas
de
suas
afetações,
sua
estranha
maneira
de
vestir-se
e
alguns
hábitos
que
podem
ter
sido
um
tanto
exibicionistas.
Afinal
de
contas,
era
admirador
e
amigo
de
Charlie Chaplin.
Mas
nenhuma
dessas
atividades
desviava
Einstein
de
seus
estudos
mais
sérios.
O
ano
de
1922
fora
testemunha
de
outra
confirmação
espetacular
de
seus
conceitos
sobre
os
quanta,
quando
o
físico
norte-americano
Arthur
Holly
Compton
(1892-1967)
descobriu
que
os
Raios
-
X
eram
difundidos
por
elétrons
livres
como
partículas
com
uma
energia
hv
e
com
um
momentum
hv/c,
conforme
Einstein
havia
predito.
Particularmente,
o
quantum
difundido
tinha
uma
frequência
diferente,
que
variava
de
acordo
com
o
angulo
de
difusão.
Eram
fatos
que
a
teoria
ondulatória
não
poderia
explicar.
A
dualidade
onda-corpúsculo
da
luz
estava-se
tornando
cada
vez
mais
evidente,
quando
um
físico
indiano
desconhecido,
Satiendranath
(S.N.)
Bose
(1894-1974),
apresentou
um
manuscrito
a
Einstein
em
busca
de
sua
opinião.
O
manuscrito
continha
uma
nova
confirmação
da
fórmula
do
corpo-negro,
obtida
através
da
mecânica
estatística;
mas
Bose
considerava
quanta
de
luz,
aos
quais
aplicava
a
mecânica
estatística,
de
uma
forma
diferente
da
usual.
A
diferença
básica
é
que,
na
mecânica
estatística
de
Boltzmann,
cada
molécula
tem
uma
individualidade;
portanto,
podemos
designar
cada
uma
por
um
nome
e
assim
reconhecê-la.
Em
contraste,
para
Bose,
os
quanta
de
luz
são
absolutamente
idênticos.
Para
Boltzmann
a
troca
da
molécula
A
pela
molécula
B
permite
uma
nova
configuração,
que
deve
ser
considerada
à
parte;
mas
para
Bose
a
troca
de
dois
quanta
idênticos
não
implica
outra
configuração.
O
resultado
é
uma
nova
confirmação
da
fórmula
do
corpo-negro.
Einstein
leu
o
trabalho
que
Bose
lhe
havia
enviado,
traduziu-o
e
fez
com
que
fosse
publicado
em
um
periódico
alemão,
acrescentando
algumas
palavras
de
louvor
e
o
comentário
de
que
o
que
Bose
tinha
feito
pelos
quanta
de
luz
ele
mesmo,
Einstein,
demonstraria
ser
também
possível
para
as
moléculas.
Einstein
manteve
a
promessa
e
em
1924
publicou
um
trabalho
sobre
o
tema.
Assim
surgiram
as
novas
estatísticas,
que
seriam
complementadas
dois
anos
depois
pela
obra
de
Fermi
e
Dirac,
que
mostraram
não
serem
as
estatísticas
de
Bose
e
de
Einstein
as
únicas
possíveis,
mas
que,
na
natureza,
existem
os
dois
tipos.
Trataremos
dessa questão mais adiante, quando falarmos de Fermi.
Como
era
de
se
esperar,
Einstein
também
calculou
as
flutuações
de
um
gás
Bose-Einstein
e
mais
uma
vez
descobriu
um
indício
da
natureza dual não apenas dos quanta, mas também — e aí vinha uma novidade — das moléculas.
A
dualidade
onda-corpúsculo
estava-se
tornando
cada
vez
mais
evidente
a
partir
da
nuvem
de
mistério
em
que
estava
envolvida.
Mais
ou
menos
naquela
época,
L.
de
Broglie
fez
progressos
decisivos
nesse
campo,
mas
aqui
também
a
contribuição
de
Einstein
foi
muito
importante,
sobretudo em seu papel de avalista de conceitos novos e surpreendentes.
À
proporção
que
a
fama
de
Einstein
crescia,
ele
ia
fazendo
pronunciamentos
políticos
e
humanitários
com
maior
frequência.
Também
assumiu
uma
posição
firme
de
pacifista
e
de
defensor
do
Estado
de
Israel.
Quando
Israel
foi
criado,
muitos
anos
mais
tarde,
ofereceram
a
Einstein
o
cargo
de
Presidente,
mas,
sabendo
de
suas
próprias
qualidades
e
limitações,
ele
declinou
do
convite.
Qualquer
boa
causa
podia
ganhar
o
apoio
de
Einstein,
do
mesmo
modo
como
qualquer
bom
físico
que
ele
conhecesse
poderia
obter
uma
recomendação
de
sua
parte.
Assim,
ironicamente,
qualquer recomendação feita por Einstein, que prima facie deveria significar muito, passou a não ter valor.
Em
1927,
a
mecânica
quântica
não-relativista
já
poderia
ser
considerada
completa
e
as
primeiras
linhas
de
sua
interpretação,
segundo
a
famosa
interpretação
de
Copenhague,
já
haviam
sido
formuladas.
Bohr
apresentou
um
documento
a
esse
respeito
à
Conferência
Internacional
de
Física,
realizada
em
Como
para
celebrar
o
centenário
de
Volta.
Einstein
não
compareceu
à
Conferência
porque
não
queria
visitar
a
Itália
fascista,
mas
pouco
mais
tarde,
quando
Bohr
repetiu
as
mesmas
ideias
no
Conselho
Solvay,
recebeu
a
oposição
de
Einstein.
Bohr,
que
muitas
vezes
se
inspirara
em
Einstein,
tinha
por
ele
verdadeira
idolatria,
e
Einstein
já
fizera
repetidas
manifestações
de
admiração
e
apreço
por
seu
colega.
A
rejeição
de
Einstein
aos
mais
caros
conceitos
de
Bohr
deixaram-no
amargurado
e
desorientado.
Surgiu
daí
um
longo
debate,
durante
o
qual
Bohr
destruiu
todas
as
objeções
apresentadas
por
Einstein,
mas
teve
de
enfrentar
outras,
sem,
contudo,
conseguir
convencê-lo.
Até
o
fim
da
vida,
Einstein,
um
dos
grandes
criadores
da
física
quântica,
manteve-se
cético
quanto
à
interpretação
de
Copenhague,
embora
estivesse
ficando
cada
vez
mais
isolado
em
seu
ponto
de vista.
Com
a
ascensão
do
nazismo,
Einstein
finalmente
emigrou
da
Alemanha,
onde
sem
dúvida
alguma
teria
sido
morto,
e,
depois
de
alguma
peregrinação,
fixou-se
no
Instituto
de
Estudos
Avançados
de
Princeton,
New
Jersey.
A
chama
de
seu
gênio
estava-se
enfraquecendo
e
Einstein,
que
durante
décadas
enxergara
mais
à
frente
do
que
qualquer
outro
homem
e
introduzira
algumas
das
mais
profundas
e
mais
profícuas
ideias
no
campo
da
física,
passou
a
dedicar-se
a
problemas
que
aparentemente
não
tinham
solução
e
que
talvez
estivessem
sendo
colocados
de
forma
errônea.
As
linhas mestras da nova física que se originaram em Berna Zurique e Berlim não tiveram sequência a partir de Princeton.
Não
obstante,
Einstein
ainda
estava
destinado
a
desempenhar
um
papel
importante,
embora
paradoxal
para
um
pacifista:
pressionar
os
Estados
Unidos
para
que
fosse
construída
a
bomba
atômica.
Chamo
esse
papel
de
paradoxal,
mas
trata-se
de
posição
que
se
enquadrava
em
seus
próprios
princípios
nas
circunstâncias
da
Segunda
Guerra
Mundial.
Mas
era
um
passo
mais
político
do
que
técnico:
Einstein
certamente
não
estava
em
dia
com
a
física
nuclear
da
década
de
quarenta,
nem
contribuiu
tecnicamente
para
o
desenvolvimento
da
energia
atômica.
Em
18
de
abril
de
1955, terminou seus dias tranquilamente, em Princeton, aos setenta e seis anos de idade.
A
respeito
de
si
próprio,
certa
vez
afirmou
o
seguinte:
"Deus
é
inexorável
no
oferecimento
de
dons.
Deu-me
apenas
a
teimosia
de
uma
mula. Não! Deu-me também um agudo sentido de odor!"
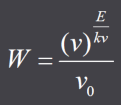
Einstein
nasceu
em
Ulm,
em
14
de
março
de
1879,
de
uma
família
judia
alemã
na
qual
predominavam
ideias
liberais.
O
pai
era
engenheiro,
mas
não
teve
sucesso
do
ponto
de
vista
financeiro.
Albert
passou
a
infância
em
Munique
e,
embora
em
casa
revelasse
indícios
de
precocidade,
na
escola
não
foi
um
aluno
excepcional.
No
curso
secundário,
não
apreciava
os
métodos
alemães
de
ensino
e
discutia
com
os
professores
que,
por
sua
vez,
o
tratavam
mal.
A
partir
dessas
primeiras
experiencias,
desenvolveu
ele
uma
constante
sensação
de
hostilidade
para
com
a
Alemanha
imperial.
Condições
desfavoráveis
em
termos
de
negócios
levaram
a
família
a
emigrar
para
Milão
em
1894
e
Einstein,
que
ficara
em
Munique
para
concluir
os
estudos,
alegou
estar
doente
para
poder
reunir-se
à
família,
na
Itália.
Gostou
mais
daquele
país
e,
durante
o
curto
período
que
ali
passou
fez
uma
viagem
a
pé
de
Milão
até
Gênova,
ou
seja,
uma
distância
de
aproximadamente 161 km.
Posteriormente,
tentou
entrar
para
a
Escola
Politécnica
de
Zurique
(Eidgenossische
Technische
Hochschule
ou
ETH),
mas
negaram-lhe
a
matrícula.
Ele
não
apenas
não
tinha
o
necessário
diploma
do
curso
secundário,
como
também
foi
reprovado
no
exame
de
admissão,
embora
se
tivesse
saído
muito
bem
em
matemática
e
física.
Para
conseguir
matricular-se,
estudou
no
ginásio
de
Aarau.
Ali
foi
muito
feliz
e
apaixonou-se
pela
Suíça,
tendo,
mais
tarde,
adotado
a
cidadania
suíça,
que
manteve
pelo
resto
da
vida.
Quando,
finalmente,
entrou
para
a
Escola
Politécnica
de
Zurique,
seus
professores
de
matemática
eram
H.
Minkowski
e
A.
Hurwitz,
scholars
de
primeira
categoria,
mas
aprendeu
muito
pouco
com
eles,
que
nem
chegaram
a
dar-se
conta
de
sua
presença.
No
entanto,
Einstein
já
tinha
dado
início
a
suas
meditações
solitárias
sobre
os
grandes
problemas
da
física
moderna,
unindo
a
inspiração
a
informações
retiradas
de
suas
próprias leituras. Fez amizade com um colega de estudos, Marcel Grossmann, um suíço que

Albert
Einstein,
fotografia
oficial
do
Prêmio
Nobel de Física de 1921.
depois
veio
a
ser
professor
de
matemática
de
respeitável
reputação.
Einstein
gostava
mais
do
laboratório
de
física
prática,
onde
podia
ver
fenômenos
com seus próprios olhos, do que dos símbolos matemáticos.
Ao
graduar-se,
teve
dificuldade
em
encontrar
emprego;
de
início,
trabalhou
como
professor
substituto
e
dava
aulas
particulares
de
física.
Em
1902,
a
família
Grossmann
conseguiu
lhe
um
emprego
modesto
no
escritório
federal
de
patentes
no
Cantão
de
Berna.Mais
ou
menos
nessa
época,
Einstein
casou-se
com
Mileva
Maric.
Tiveram
dois
filhos,
um
dos
quais
veio
a
ser
professor
de
engenharia
altamente
conceituado
da
Universidade da Califórnia, em Berkeley.
O
emprego
no
escritório
de
patentes
servia
perfeitamente
para
Einstein.
Enquanto
se
desincumbia
de
suas
funções
no
escritório,
examinando
as
invenções
que
lhe
eram
encaminhadas,
também
achava
tempo
para
pensar
sem
ser
perturbado.
Mais
tarde,
aconselhou
os
jovens
a
procurarem
empregos
semelhantes,
pois,
segundo
ele,
tais
empregos
davam
tempo
para
pensar
e,
por
isso,
eram
os
mais
apropriados
para
as
pessoas
que
tivessem
ideias
originais.
Começou
a
escrever
artigos
sobre
física,
que
enviava
para
o
Annalen
der
Physik,
então
sob
a
direção
de
W.
Wien,
já
famoso
por
seus
estudos
sobre
o
corpo-
negro.
Apresentou
um
trabalho
em
1901,
dois
em
1902,
um
em
1903
e
um
em
1904.
Eram
estudos
profundos
na
área
da
termodinâmica
e
da
mecânica
estatística.
Mas,
sem
que
Einstein
o
soubesse,
o
trabalho
já
havia
sido
realizado
por
Gibbs;
coisa
parecida ocorreu com o de Planck alguns anos mais tarde.
Em
1905,
o
gênio
de
Einstein
eclodiu
com
uma
luminosidade
insuperada.
Em
março,
maio
e
junho
ele
escreveu
três
obras,
cada
uma
das
quais,
sozinha,
teria
sido
suficiente
para
imortalizá-lo.
Somente
Newton,
aos
vinte
e
três
anos
de
idade,
confinado
pela
praga
que
devastava
sua
aldeia
de
Woolsthorpe,
tivera
um
vigor
semelhante.
A
primeira
obra—
"
Uber
einen
die
Erzeugung
und
Verwandlung
des
Lichts
berrefenden
heuristischen
Gesichts-
punkt"
("Um
ponto
de
vista
heurístico
sobre
a
geração
e
transformação
da
luz")
—
contém
a
descoberta
dos
quanta
de
luz
e,
como
aplicação
secundária,
a
explicação
do
efeito
fotoelétrico.
A
segunda
—
"Uber
die
von
der
Molekularkinetischen
suspendierten
Teilchen'”
("Sobre
os
movimentos
de
partículas
suspensas
em
líquidos
em
repouso
conforme
a
teoria
cinética
do
calor")
—
contém
a
teoria
do
movimento
browniano,
mostra
mais
uma
vez
a
existência
real
dos
átomos
e
determina
a
constante
de
Boltzmann
de
uma
nova
maneira.
A
terceira—
"
Zur
Elektrodynamik
bewegter
Kôrper"
("Sobre
a
eletrodinâmica
dos
corpos
em
movimento")
contém
a
teoria
específica
da
relatividade,
da
qual
sai
a
famosa
fórmula
E
=
mc
2
que
é
praticamente
tudo
o
que
o
público
sabe
a
respeito
de
Einstein.
A
verdade
é
que
há
algumas
pessoas
que
acreditam
que
esse
é
"o
segredo
da
bomba
atômica". É um segredo, no entanto, que não mais existe, da mesma forma que o unicórnio: ambos são produtos da imaginação.
Essas
obras,
sobre
temas
diferentes,
têm
alguma
característica
em
comum
que
deriva
da
personalidade
científica
de
Einstein.
São
revolucionárias,
abertas
e
fazem
uso
de
métodos
matemáticos
simples.
Ele
alcança
resultados
inteiramente
surpreendentes
aplicando
uma
lógica
descompromissada, solidamente baseada em experiências.
Primeiro
tratarei
da
terceira
obra,
sobre
relatividade.
Dela
emergiram
grandes
consequências
práticas
que
vão
do
equilíbrio
da
energia
em
uma
bomba
atômica
bem
como
no
sol,
até
a
dinâmica
necessária
à
construção
de
grandes
aceleradores
de
partículas.
Acima
de
tudo,
esse
documento
provocou
uma
revolução
em
nossos
conceitos
de
tempo
e
espaço.
Durante
séculos,
os
filósofos
tinham
tentado
analisar
esses
conceitos
sem nunca chegarem a resultados tão profundos e tão definitivos quanto os de Einstein.
Para
facilitar
o
entendimento
desta
e
de
outras
obras
de
Einstein,
precisarei
fazer
uma
breve
digressão
a
respeito
da
luz.
O
estudo
científico
da
luz
começou
na
Renascença
e
atingiu
o
auge
na
época
de
Newton
e
de
C.
Huygens.
Esses
dois
grandes
expoentes
dos
primórdios
da
física
pós-Galileu
tinham
formulado
teorias
conflitantes
sobre
a
luz.
Segundo
Newton,
a
luz
era
constituída
de
projéteis
que
se
moviam
a
grande
velocidade;
segundo
Huygens,
era
composta
de
ondas
propagadas
em
um
meio
bastante
delicado,
o
éter.
Durante
anos,
ambas
as
teorias
permaneceram
conflitantes,
mas,
no
início
do
século
XIX,
demonstrou-se
que
a
luz
podia
mostrar
fenômenos
de
interferência,
isto
é,
acrescentando-se
luz
à
luz,
podia-se
obter
escuridão.
Essa
ocorrência
é
facilmente
explicada
pela
teoria
das
ondas,
porque
duas
ondas
de
fases
opostas
e
da
mesma
amplitude
podem
destruir-se
uma
à
outra
—
as
cristas
de
uma
enchendo
os
cavados
da
outra.
Mas
a
interferência
não
pode
ser
explicada
com
a
teoria
corpuscular.
Além
do
mais,
a
teoria
das
ondas
exige
que
nos
fenômenos
de
refração
a
luz
seja
propagada
mais
lentamente
em
meios
mais
densos,
enquanto na teoria corpuscular ocorre o contrário. Também a esse respeito as experiências favorecem a teoria das ondas.
Mais
tarde,
as
equações
de
Maxwell,
que
pareciam
quase
sobre-humanas
em
sua
força
e
generalidade,
explicaram
todos
os
fenômenos
da
luz
conhecidos.
A
velocidade
da
propagação
podia
relacionar-se
com
quantidades
elétricas
que
podiam
ser
medidas
em
laboratório
por
instrumentos
elétricos
como
condensadores,
galvanômetros
e
ímãs,
que
não
pareciam
ter
qualquer
relação
com
a
luz.
Como
a
luz
foi
reduzida
a
vibrações
elétricas
do
éter,
surgiu
o
problema
de
determinar
as
propriedades
do
éter.
Em
algumas
teorias,
o
éter
era
dotado
de
propriedades
mecânicas específicas, como um coeficiente de elasticidade. De qualquer modo, todas as teorias precisavam de alguma espécie de éter.
Se
uma
fonte
de
luz
ou
um
observador
move-se
em
relação
ao
éter,
esse
movimento
deve
de
alguma
forma
manifestar-se.
No
caso
do
som
propagado
no
ar,
quando
uma
fonte
se
move
com
a
velocidade
do
som
em
relação
ao
ar
em
repouso
(mach
l),
ocorrem
efeitos
espetaculares,
que
já
foram
chamados
de
barreira
do
som.
Por
outro
lado,
não
se
poderia
observar
nada
que
mostrasse
um
movimento
relativo
ao
éter.
Por
exemplo,
tinha-se
descoberto
que
a
velocidade
de
propagação
da
luz
no
vácuo
é
sempre
vácuo
é
sempre
c
=
2,997924
X
10
10
cm/seg.
Esse
resultado
fora
constatado
com
precisão
por
A.A.
Michelson
e
mais
tarde
por
Michelson
e
E.
W.
Morley,
que
tinham
realizado
medições
com
um
dos
interferômetros de Michelson orientado em várias direções em relação à direção do movimento da
terra.
Michelson
(1852-1931)
nasceu
em
Strelno
(então
Prússia),
mas
a
família
emigrou
para
a
Califórnia
quando
ele
ainda
era
criança,
e
Michelson
cresceu
em
uma
cidade
mineira
semelhante
àquelas
vistas
nos
filmes
de
faroeste.
Foi
para
a
Academia
Naval
de
Anápolis,
onde
se
graduou
como
guarda-marinha.
Seu
treinamento
militar
foi
seguido
por
uma
longa
e
brilhante
carreira
científica
que
o
tornou
um
dos
mais
famosos
físicos
norte-
americanos
e
o
primeiro
norte-americano
a
ser
laureado
com
o
Prêmio
Nobel.
Suas
medições
da
velocidade
da
luz
são
um
dos
pilares
da
teoria
da
relatividade, conforme é ensinada atualmente, mas, ao que tudo indica, não teriam influenciado Einstein em 1905.
Einstein
provavelmente
estava
convencido
a
priori
de
que
as
equações
de
Maxwell
tinham
exatamente
a
mesma
forma
em
todos
os
sistemas
de
referência
em
movimento
retilíneo
uniforme
com
relação
uns
aos
outros.
Talvez
tenha
chegado
a
suas
conclusões
ainda
jovem,
enquanto
meditava
sobre
como
uma
onda
eletromagnética
apareceria
a
um
observador
que
a
estivesse
seguindo
a
uma
velocidade
c.
De
qualquer
modo,
para
ele
a
constância
da
velocidade
da
luz
era
indiscutível.
Tinha
de
ser
a
mesma
em
todos
os
sistemas
de
referência,
embora
Einstein
provavelmente
não
conhecesse
a
confirmação
direta
de
Michelson,
pois
não
a
cita
em
seu
documento
de
1905.
A
postulação
axiomática
de
Einstein
do
princípio
da
relatividade faz lembrar os princípios da termodinâmica e afirma:
1)
Postulado
da
relatividade:
Não
é
possível
distinguir
um
sistema
de
referência
de
outro
movendo-se
com
velocidade
constante
em
magnitude
e
direção
em
relação
a
ele.
Tais
sistemas
são
chamados
de
inerciais.
O
termo
distinguir
significa
que
cada
experiência
realizada
no
primeiro
ou
no
segundo sistema dá o mesmo resultado para um observador relacionado com o sistema.
2) Postulado da constância da velocidade da luz:
A velocidade da luz é independente do movimento de sua fonte.
Os
físicos
anteriores
a
Einstein
tinham
enfrentado
as
dificuldades
apresentadas
pela
eletrodinâmica
dos
corpos
em
movimento.
Hertz,
entre
outros,
procurara
dar-lhe
uma
formulação.
Lorentz,
G.
F.
Fitz
-
Gerald
e
Poincaré
tinham
dedicado
muita
atenção
ao
assunto.
Lorentz
julgava
que
as
equações
de
Maxwell
não
mantêm
a
mesma
forma
quando
passam
de
um
sistema
de
referência
a
outro,
segundo
as
regras
dadas
por
Galileu
e,
aparentemente,
baseadas
no
bom
senso.
Chamando-se
de
x
a
coordenada
de
espaço
e
de
t
o
tempo
no
primeiro
sistema;
e
de
x'
e
t'
as
quantidades
correspondentes
no
segundo
sistema,
que
se
move
a
uma
velocidade
v
em
relação
ao
primeiro
sistema,
as
equações
de
transformação
de
Galileu
ficam:
x' = x — vt
t = t’
Transformando
as
coordenadas
de
um
sistema
para
um
outro
segundo
essas
regras,
observam-se
mudanças
dignas
de
nota
nas
equações de Maxwell. Ressalta-se particularmente que o tempo é o mesmo nos dois sistemas.
Lorentz
tinha
descoberto
uma
transformação
de
coordenadas,
a
famosa
transformação
de
Lorentz,
que
deixa
as
equações
de
Maxwell
invariantes e, quando
v << c,
reduz-se à transformação de Galileu, é expressa pelas seguintes equações:
A transformação de Lorentz é correta, mas, à época, parecia ser pouco mais do que um recurso matemático.





Em sua famosa carta ao cientista Arnold Sommerfeld, de 28 de novembro de 1915…. …Einstein comunica pela primeira vez a fórmula

EINSTEIN: NOVAS FORMAS DE PENSAR
Se
Rafael
pudesse
voltar
à
vida,
certamente
pintaria
uma
moderna
Escola
de
Atenas
de
físicos.
E
naturalmente
incluiria
Einstein
junto
com Galileu, Newton e Maxwell apontando para o céu, enquanto Faraday e Rutherford apontariam para a terra.
Emílio Gino Segré




Leitura



Índice dos textos

© CIÊNCIA-CULTURA.COM - Responsável - Ricardo Pante

Albert
Einstein,
fotografia
oficial
do
Prêmio
Nobel
de Física de 1921.
Einstein
nasceu
em
Ulm,
em
14
de
março
de
1879,
de
uma
família
judia
alemã
na
qual
predominavam
ideias
liberais.
O
pai
era
engenheiro,
mas
não
teve
sucesso
do
ponto
de
vista
financeiro.
Albert
passou
a
infância
em
Munique
e,
embora
em
casa
revelasse
indícios
de
precocidade,
na
escola
não
foi
um
aluno
excepcional.
No
curso
secundário,
não
apreciava
os
métodos
alemães
de
ensino
e
discutia
com
os
professores
que,
por
sua
vez,
o
tratavam
mal.
A
partir
dessas
primeiras
experiencias,
desenvolveu
ele
uma
constante
sensação
de
hostilidade
para
com
a
Alemanha
imperial.
Condições
desfavoráveis
em
termos
de
negócios
levaram
a
família
a
emigrar
para
Milão
em
1894
e
Einstein,
que
ficara
em
Munique
para
concluir
os
estudos,
alegou
estar
doente
para
poder
reunir-se
à
família,
na
Itália.
Gostou
mais
daquele
país
e,
durante
o
curto
período
que
ali
passou
fez
uma
viagem
a
pé
de
Milão
até
Gênova,
ou
seja,
uma
distância
de
aproximadamente 161 km.
Posteriormente,
tentou
entrar
para
a
Escola
Politécnica
de
Zurique
(Eidgenossische
Technische
Hochschule
ou
ETH),
mas
negaram-lhe
a
matrícula.
Ele
não
apenas
não
tinha
o
necessário
diploma
do
curso
secundário,
como
também
foi
reprovado
no
exame
de
admissão,
embora
se
tivesse
saído
muito
bem
em
matemática
e
física.
Para
conseguir
matricular-se,
estudou
no
ginásio
de
Aarau.
Ali
foi
muito
feliz
e
apaixonou-se
pela
Suíça,
tendo,
mais
tarde,
adotado
a
cidadania
suíça,
que
manteve
pelo
resto
da
vida.
Quando,
finalmente,
entrou
para
a
Escola
Politécnica
de
Zurique,
seus
professores
de
matemática
eram
H.
Minkowski
e
A.
Hurwitz,
scholars
de
primeira
categoria,
mas
aprendeu
muito
pouco
com
eles,
que
nem
chegaram
a
dar-se
conta
de
sua
presença.
No
entanto,
Einstein
já
tinha
dado
início
a
suas
meditações
solitárias
sobre
os
grandes
problemas
da
física
moderna,
unindo
a
inspiração
a
informações
retiradas
de
suas
próprias
leituras.
Fez
amizade
com
um
colega
de
estudos,
Marcel
Grossmann,
um
suíço
que
depois
veio
a
ser
professor
de
matemática
de
respeitável
reputação.
Einstein
gostava
mais
do
laboratório
de
física
prática,
onde
podia
ver
fenômenos
com
seus
próprios
olhos, do que dos símbolos matemáticos.
Ao
graduar-se,
teve
dificuldade
em
encontrar
emprego;
de
início,
trabalhou
como
professor
substituto
e
dava
aulas
particulares
de
física.
Em
1902,
a
família
Grossmann
conseguiu
lhe
um
emprego
modesto
no
escritório
federal
de
patentes
no
Cantão
de
Berna.Mais
ou
menos
nessa
época,
Einstein
casou-se
com
Mileva
Maric.
Tiveram
dois
filhos,
um
dos
quais
veio
a
ser
professor
de
engenharia
altamente
conceituado
da
Universidade da Califórnia, em Berkeley.
O
emprego
no
escritório
de
patentes
servia
perfeitamente
para
Einstein.
Enquanto
se
desincumbia
de
suas
funções
no
escritório,
examinando
as
invenções
que
lhe
eram
encaminhadas,
também
achava
tempo
para
pensar
sem
ser
perturbado.
Mais
tarde,
aconselhou
os
jovens
a
procurarem
empregos
semelhantes,
pois,
segundo
ele,
tais
empregos
davam
tempo
para
pensar
e,
por
isso,
eram
os
mais
apropriados
para
as
pessoas
que
tivessem
ideias
originais.
Começou
a
escrever
artigos
sobre
física,
que
enviava
para
o
Annalen
der
Physik,
então
sob
a
direção
de
W.
Wien,
já
famoso
por
seus
estudos
sobre
o
corpo-
negro.
Apresentou
um
trabalho
em
1901,
dois
em
1902,
um
em
1903
e
um
em
1904.
Eram
estudos
profundos
na
área
da
termodinâmica
e
da
mecânica
estatística.
Mas,
sem
que
Einstein
o
soubesse,
o
trabalho
já
havia
sido
realizado
por
Gibbs;
coisa
parecida
ocorreu
com o de Planck alguns anos mais tarde.
Em
1905,
o
gênio
de
Einstein
eclodiu
com
uma
luminosidade
insuperada.
Em
março,
maio
e
junho
ele
escreveu
três
obras,
cada
uma
das
quais,
sozinha,
teria
sido
suficiente
para
imortalizá-lo.
Somente
Newton,
aos
vinte
e
três
anos
de
idade,
confinado
pela
praga
que
devastava
sua
aldeia
de
Woolsthorpe,
tivera
um
vigor
semelhante.
A
primeira
obra—
"
Uber
einen
die
Erzeugung
und
Verwandlung
des
Lichts
berrefenden
heuristischen
Gesichts-
punkt"
("Um
ponto
de
vista
heurístico
sobre
a
geração
e
transformação
da
luz")
—
contém
a
descoberta
dos
quanta
de
luz
e,
como
aplicação
secundária,
a
explicação
do
efeito
fotoelétrico.
A
segunda
—
"Uber
die
von
der
Molekularkinetischen
suspendierten
Teilchen'”
("Sobre
os
movimentos
de
partículas
suspensas
em
líquidos
em
repouso
conforme
a
teoria
cinética
do
calor")
—
contém
a
teoria
do
movimento
browniano,
mostra
mais
uma
vez
a
existência
real
dos
átomos
e
determina
a
constante
de
Boltzmann
de
uma
nova
maneira.
A
terceira—
"
Zur
Elektrodynamik
bewegter
Kôrper"
("Sobre
a
eletrodinâmica
dos
corpos
em
movimento")
contém
a
teoria
específica
da
relatividade,
da
qual
sai
a
famosa
fórmula
E
=
mc
2
que
é
praticamente
tudo
o
que
o
público
sabe
a
respeito
de
Einstein.
A
verdade
é
que
há
algumas
pessoas
que
acreditam
que
esse
é
"o
segredo
da
bomba
atômica".
É
um
segredo,
no
entanto,
que
não
mais
existe,
da
mesma
forma
que
o
unicórnio: ambos são produtos da imaginação.
Essas
obras,
sobre
temas
diferentes,
têm
alguma
característica
em
comum
que
deriva
da
personalidade
científica
de
Einstein.
São
revolucionárias,
abertas
e
fazem
uso
de
métodos
matemáticos
simples.
Ele
alcança
resultados
inteiramente
surpreendentes
aplicando
uma
lógica
descompromissada,
solidamente
baseada em experiências.
Primeiro
tratarei
da
terceira
obra,
sobre
relatividade.
Dela
emergiram
grandes
consequências
práticas
que
vão
do
equilíbrio
da
energia
em
uma
bomba
atômica
bem
como
no
sol,
até
a
dinâmica
necessária
à
construção
de
grandes
aceleradores
de
partículas.
Acima
de
tudo,
esse
documento
provocou
uma
revolução
em
nossos
conceitos
de
tempo
e
espaço.
Durante
séculos,
os
filósofos
tinham
tentado
analisar
esses
conceitos
sem
nunca
chegarem
a
resultados
tão
profundos
e
tão
definitivos quanto os de Einstein.
Para
facilitar
o
entendimento
desta
e
de
outras
obras
de
Einstein,
precisarei
fazer
uma
breve
digressão
a
respeito
da
luz.
O
estudo
científico
da
luz
começou
na
Renascença
e
atingiu
o
auge
na
época
de
Newton
e
de
C.
Huygens.
Esses
dois
grandes
expoentes
dos
primórdios
da
física
pós-Galileu
tinham
formulado
teorias
conflitantes
sobre
a
luz.
Segundo
Newton,
a
luz
era
constituída
de
projéteis
que
se
moviam
a
grande
velocidade;
segundo
Huygens,
era
composta
de
ondas
propagadas
em
um
meio
bastante
delicado,
o
éter.
Durante
anos,
ambas
as
teorias
permaneceram
conflitantes,
mas,
no
início
do
século
XIX,
demonstrou-se
que
a
luz
podia
mostrar
fenômenos
de
interferência,
isto
é,
acrescentando-se
luz
à
luz,
podia-se
obter
escuridão.
Essa
ocorrência
é
facilmente
explicada
pela
teoria
das
ondas,
porque
duas
ondas
de
fases
opostas
e
da
mesma
amplitude
podem
destruir-se
uma
à
outra
—
as
cristas
de
uma
enchendo
os
cavados
da
outra.
Mas
a
interferência
não
pode
ser
explicada
com
a
teoria
corpuscular.
Além
do
mais,
a
teoria
das
ondas
exige
que
nos
fenômenos
de
refração
a
luz
seja
propagada
mais
lentamente
em
meios
mais
densos,
enquanto
na
teoria
corpuscular
ocorre
o
contrário.
Também
a
esse
respeito
as
experiências
favorecem a teoria das ondas.
Mais
tarde,
as
equações
de
Maxwell,
que
pareciam
quase
sobre-humanas
em
sua
força
e
generalidade,
explicaram
todos
os
fenômenos
da
luz
conhecidos.
A
velocidade
da
propagação
podia
relacionar-
se
com
quantidades
elétricas
que
podiam
ser
medidas
em
laboratório
por
instrumentos
elétricos
como
condensadores,
galvanômetros
e
ímãs,
que
não
pareciam
ter
qualquer
relação
com
a
luz.
Como
a
luz
foi
reduzida
a
vibrações
elétricas
do
éter,
surgiu
o
problema
de
determinar
as
propriedades
do
éter.
Em
algumas
teorias,
o
éter
era
dotado
de
propriedades
mecânicas
específicas,
como
um
coeficiente
de
elasticidade.
De
qualquer
modo,
todas as teorias precisavam de alguma espécie de éter.
Se
uma
fonte
de
luz
ou
um
observador
move-se
em
relação
ao
éter,
esse
movimento
deve
de
alguma
forma
manifestar-se.
No
caso
do
som
propagado
no
ar,
quando
uma
fonte
se
move
com
a
velocidade
do
som
em
relação
ao
ar
em
repouso
(mach
l),
ocorrem
efeitos
espetaculares,
que
já
foram
chamados
de
barreira
do
som.
Por
outro
lado,
não
se
poderia
observar
nada
que
mostrasse
um
movimento
relativo
ao
éter.
Por
exemplo,
tinha-se
descoberto
que
a
velocidade
de
propagação
da
luz
no
vácuo
é
sempre
vácuo
é
sempre
c
=
2,997924
X
10
10
cm/seg.
Esse
resultado
fora
constatado
com
precisão
por
A.A.
Michelson
e
mais
tarde
por
Michelson
e
E.
W.
Morley,
que
tinham
realizado
medições
com
um
dos
interferômetros
de
Michelson
orientado
em
várias
direções
em
relação
à
direção
do
movimento
da
terra.
Michelson
(1852-1931)
nasceu
em
Strelno
(então
Prússia),
mas
a
família
emigrou
para
a
Califórnia
quando
ele
ainda
era
criança,
e
Michelson
cresceu
em
uma
cidade
mineira
semelhante
àquelas
vistas
nos
filmes
de
faroeste.
Foi
para
a
Academia
Naval
de
Anápolis,
onde
se
graduou
como
guarda-marinha.
Seu
treinamento
militar
foi
seguido
por
uma
longa
e
brilhante
carreira
científica
que
o
tornou
um
dos
mais
famosos
físicos
norte-americanos
e
o
primeiro
norte-americano
a
ser
laureado
com
o
Prêmio
Nobel.
Suas
medições
da
velocidade
da
luz
são
um
dos
pilares
da
teoria
da
relatividade,
conforme
é
ensinada
atualmente,
mas,
ao
que
tudo
indica,
não
teriam
influenciado Einstein em 1905.
Einstein
provavelmente
estava
convencido
a
priori
de
que
as
equações
de
Maxwell
tinham
exatamente
a
mesma
forma
em
todos
os
sistemas
de
referência
em
movimento
retilíneo
uniforme
com
relação
uns
aos
outros.
Talvez
tenha
chegado
a
suas
conclusões
ainda
jovem,
enquanto
meditava
sobre
como
uma
onda
eletromagnética
apareceria
a
um
observador
que
a
estivesse
seguindo
a
uma
velocidade
c.
De
qualquer
modo,
para
ele
a
constância
da
velocidade
da
luz
era
indiscutível.
Tinha
de
ser
a
mesma
em
todos
os
sistemas
de
referência,
embora
Einstein
provavelmente
não
conhecesse
a
confirmação
direta
de
Michelson,
pois
não
a
cita
em
seu
documento
de
1905.
A
postulação
axiomática
de
Einstein
do
princípio
da
relatividade
faz
lembrar
os
princípios da termodinâmica e afirma:
1)
Postulado
da
relatividade:
Não
é
possível
distinguir
um
sistema
de
referência
de
outro
movendo-se
com
velocidade
constante
em
magnitude
e
direção
em
relação
a
ele.
Tais
sistemas
são
chamados
de
inerciais.
O
termo
distinguir
significa
que
cada
experiência
realizada
no
primeiro
ou
no
segundo
sistema
dá
o
mesmo
resultado
para um observador relacionado com o sistema.
2)
Postulado
da
constância
da
velocidade
da
luz:
A
velocidade
da
luz
é
independente
do
movimento
de
sua
fonte.
Os
físicos
anteriores
a
Einstein
tinham
enfrentado
as
dificuldades
apresentadas
pela
eletrodinâmica
dos
corpos
em
movimento.
Hertz,
entre
outros,
procurara
dar-lhe
uma
formulação.
Lorentz,
G.
F.
Fitz
-
Gerald
e
Poincaré
tinham
dedicado
muita
atenção
ao
assunto.
Lorentz
julgava
que
as
equações
de
Maxwell
não
mantêm
a
mesma
forma
quando
passam
de
um
sistema
de
referência
a
outro,
segundo
as
regras
dadas
por
Galileu
e,
aparentemente,
baseadas
no
bom
senso.
Chamando-se
de
x
a
coordenada
de
espaço
e
de
t
o
tempo
no
primeiro
sistema;
e
de
x'
e
t'
as
quantidades
correspondentes
no
segundo
sistema,
que
se
move
a
uma
velocidade
v
em
relação
ao
primeiro
sistema,
as
equações
de
transformação de Galileu ficam:
x' = x — vt
t = t’
Transformando
as
coordenadas
de
um
sistema
para
um
outro
segundo
essas
regras,
observam-
se
mudanças
dignas
de
nota
nas
equações
de
Maxwell.
Ressalta-se
particularmente
que
o
tempo
é
o
mesmo
nos
dois sistemas.
Lorentz
tinha
descoberto
uma
transformação
de
coordenadas,
a
famosa
transformação
de
Lorentz,
que
deixa
as
equações
de
Maxwell
invariantes
e,
quando
v
<<
c,
reduz-se
à
transformação
de
Galileu,
é
expressa pelas seguintes equações:
A
transformação
de
Lorentz
é
correta,
mas,
à
época,
parecia
ser
pouco
mais
do
que
um
recurso
matemático.





Em
sua
famosa
carta
ao
cientista
Arnold
Sommerfeld,
de
28
de
novembro
de
1915….
…Einstein
comunica
pela
primeira
vez a fórmula
Einstein
atacou
o
problema
da
transformação
do
tempo
e
do
espaço
com
enfoque
profundo
e
entusiasmo
quase
infantil.
Com
uma
lógica
convincente,
analisou
cuidadosamente
os
conceitos
de
tempo
e
espaço
usando
um
método
operacional,
que
para
cada
conceito
introduzido,
exigia
uma
especificação
rigorosa
e
concreta
de
como
medir
as
magnitudes
envolvidas.
Naturalmente
estava
interessado
não
nos
instrumentos
e
em
mecânica,
mas
na
lógica
da
experiência.
Resultados
inteiramente
inesperados
surgiram
de
sua
análise,
como,
por
exemplo,
a
relatividade
da
simultaneidade:
fatos
que
ocorrem
em
diferentes
locais
e
ao
mesmo
tempo
para
um
observador
não
parecem
simultâneos
para
outro
que
se
mova
em
relação
ao
primeiro.
Do
mesmo
modo,
há
o
paradoxo
dos
gêmeos:
um
irmão
gêmeo
permanece
em
um
sistema
de
referência
e
o
outro
se
afasta
em
movimento
uniforme
e
retilíneo,
inverte
a
direção
do
movimento
e
retorna.
Quando
o
segundo
irmão
gêmeo
volta
a
encontrar
o
primeiro,
acha-o
mais
velho.
Se
formos
céticos
a
esse
respeito,
a
experiência
já
foi
realizada
com
partículas
que
se
desintegram,
e
o
resultado
previsto
pela
relatividade
foi
confirmado.
Acima
de
tudo,
ficou
evidente
que
não
era
a
transformação
de
Galileu,
mas
a
de
Lorentz
que
correspondia
à
maneira
correta
de
medir
o
tempo
e
o
espaço.
A
lógica
de
Einstein
é
irrefutável,
embora
à
época
soasse
desagradável
a
muitos
físicos,
em
razão
de
sua
aparente
contradição
com
a
experiência
do
quotidiano.
Sublinho
aparente
porque,
na
realidade,
essa
contradição não existe.
Um
dos
professores
de
Einstein,
Hermann
Minkowski
(1864-1909),
inventou
uma
delicada
expressão
matemática
para
a
transformação
das
coordenadas
de
espaço
e
tempo.
Introduziu
um
espaço
quadrimensional,
três
dimensões
de
espaço
e
uma
de
tempo.
A
característica
específica
desse
espaço
é
que
a
distância
entre
dois
pontos
não
é
dada
pelo
teorema
de
Pitágoras
que,
no
espaço
ordinário,
diz
espaço
que
s
2
=
x
2
+
y
2
+
z
2
.
O
espaço
quadrimensional
de
Minkowski
usa
uma
forma
um
pouco
diferente:
s
2
=
x
2
+
y
2
+
z
2
–
c
2
t
2
.
A
introdução
do
tempo
em
espaço
quadrimensional
e
o
sinal
menos
em
frente
ao
último
termo
é
que
modificam
radicalmente
a
situação.
Em
uma
conferência
histórica,
pronunciada
em
1908,
Minkowski
apresentou
seus
novos
conceitos
com as seguintes palavras:
"Cavalheiros,
as
noções
de
espaço
e
tempo
que
desejo
apresentar-lhes
emergiram
do
terreno
da
física
experimental
e
ali
reside
sua
força.
São
radicais.
Daqui
em
diante,
o
espaço
por
si
mesmo,
e
o
tempo,
por
si
mesmo,
estão
destinados
a
transformar-se
em
meras
sombras
e
apenas
uma
espécie
de
união
dos
dois
preservará
uma
realidade
independente".
(Conferência
aos
80.
Versammlung
Deutscher
Naturforscher
und
Aerzte, Colônia, 1908.)
Quando
Minkowski
viu
o
trabalho
original
de
Einstein,
lembrou-se
de
seu
aluno
e
disse
o
seguinte:
"Imaginem
só!
Eu
nunca
esperaria
uma
coisa
tão
inteligente vinda desse camarada".
As
consequências
da
teoria
da
relatividade
são
vastas,
profundas
e
inesperadas.
Segundo
o
modo
de
pensar
de
Einstein,
a
velocidade
da
luz
aparece
como
uma
constante
universal
e
seu
caráter
fundamental
transcende
sua
conexão
histórica
com
o
eletromagnetismo.
Relaciona
espaço
e
tempo
na
transformação
de
Lorentz;
é
a
velocidade
limite
que
não
pode
ser
superada
na
transmissão
de
sinais;
aparece
na
conexão
entre
velocidade,
energia
e
momentum
de
um
ponto
material
que
tem
a
massa
m
em
repouso.
Essa
conexão é dada pelas fórmulas
A
massa
dos
corpos,
definida
como
proporção
entre
força
e
aceleração,
torna-se
variável
com
a
velocidade.
A
conservação
da
massa
já
não
constitui
uma
lei
precisa
e
substitui
uma
generalização
da
conservação
da
energia,
na
qual
a
massa
pode
transformar-se em energia segundo a fórmula
mc
2
= E
Físicos modernos chegaram a descobrir
"partículas" sem massa sendo a mais notável o quantum
de luz. Para essas partículas, E = cp, e elas se movem com
a velocidade da luz em relação a qualquer sistema
inercial.


Os
novos
conceitos
desnortearam
os
físicos.
Mesmo
um
grande
físico
teórico
como
H.A.
Lorentz,
que
achara
a
transformação
básica
para
a
relatividade,
teve
dificuldade
para
aceitar
as
novas
ideias.
Não
que
a
matemática
apresentasse
um
obstáculo:
as
dificuldades
nesse
campo
eram
mínimas.
A
barreira
estava
na
verdadeira
forma
de
pensar
e,
em
consequência,
a
teoria
só
veio
a
tornar-se
familiar
para
os
físicos
uma
geração
mais
tarde.
Ideias
genuinamente
novas
em
físicas
solidificam-se
com
muita
lentidão,
sobretudo
porque
a
geração
que
as
cria
não
consegue
"senti-las".
Os
físicos
mais
amadurecidos
podem
aprender,
mas
a
verdadeira
assimilação
ocorre
quando
os
contemporâneos
morrem
e
os
sucessores
passam
a
considerar
as
ideias
novas
como
básicas.
Testemunhei
esse
fenômeno
bem
de
perto
na
mecânica
dos
quanta.
Devo
acrescentar
ainda
que
a
nova
geração,
doutrinada
desde
o
início,
não
tem
consciência
de
muitos
dos
dilemas e objeções que os criadores têm de enfrentar.
A
relatividade
só
foi
sendo
aceita
aos
poucos.
Por
exemplo,
mesmo
em
1922,
a
Academia
Sueca
concedeu
o
Prêmio
Nobel
a
Einstein
"pelo
serviço
por ele
p
restado
à
física
teórica
e
particularmente
por
sua
descoberta
da
lei
do
efeito
fotoelétrico".
Pode
parecer
estranho
que
a
relatividade
não
seja
mencionada,
mas,
numa
retrospectiva,
a
meu
ver,
houve
sabedoria
nessa
escolha.
Não
é
que
a
relatividade
seja
um
tema
de
importância
secundária,
mas
é
que
os
outros
"serviços"
de Einstein foram imensos.
Voltemos
agora
ao
primeiro
dos
dois
documentos
escritos
por
Einstein
no
surpreendente
ano
de
1905.
A
meu
ver,
é
uma
das
maiores
obras
já
realizadas
em
física.
Naquela
época,
os
cientistas
sabiam
que
a
luz
era
constituída
de
ondas
eletromagnéticas;
se
havia
alguma
coisa
de
certo,
era
isso.
No
entanto,
Einstein
tinha
dúvidas
e
revelou
a
natureza
dual
da
luz
—
corpuscular
e
ondulatória.
Essa
descoberta,
junto
com
o
aspecto
dual
correspondente
da
matéria,
tornou-se
a
maior
conquista
do
século.
Newton
e
Huygens
foram
inesperadamente
reconciliados
por
uma
profunda
revolução
na
filosofia
natural,
que
mostrou
estarem
ambos, em parte, certos.
Planck
quantizava
a
energia
dos
osciladores
que
formavam
as
paredes
de
sua
versão
do
corpo-negro.
Com
referência
à
radiação
propriamente
dita,
pôde
apenas
dar
a
expressão
u
(v,
t).
Acredito
que
ele
mesmo
não
tinha
dúvidas
de
que
as
equações
de
Maxwell
descreviam
exatamente
as
ondas
eletromagnéticas
que
enchem
a
cavidade.
Einstein,
no
entanto,
perguntava-se
se
a
descrição
de
Maxwell
era
compatível
com
a
fórmula
do
corpo-negro
de
Planck
e
chegou
à
surpreendente
conclusão
de
que
a
própria
luz
devia
ser
composta
de
quanta
quase-corpusculares.
Não
posso
deixar
de
lado
seu
raciocínio
porque,
quando
o
li,
sua
força
e
simplicidade
praticamente
me
arrasaram
quase
que
fisicamente.
Einstein
observou
que
a
derivação
de
Planck,
ao
considerar
as
trocas
de
energia
entre
osciladores
e
radiações,
pressupõe
implicitamente
que
a
energia
pode
ser
absorvida
e
emitida
pelo
oscilador
isolado
apenas
em
quanta
de
magnitude
hv,
isto
é,
que
a
energia
de
uma
estrutura
mecânica
capaz
de
oscilações,
bem
como
a
energia
da
radiação,
pode
ser
transferida
apenas
nesses
quanta,
em
contradição
com
as
leis
da
mecânica e da eletrodinâmica".
A
física
clássica
leva-nos
inevitavelmente
ao
enfoque
Rayleigh-Jeans
da
fórmula
de
Planck.
É
válido
para
hv/kt
<<
1,
e
nela
h
não
aparece.
Para
hv/kt
>>
1,
a
fórmula
de
Wien
é
válida,
e
os
conceitos
clássicos
fracassam.
Einstein
concentrou
sua
atenção
na
fórmula
de
Wien
e
a
partir
dela
obteve
uma
expressão
para
a
entropia
de
uma
radiação
de
certa
frequência
contida
em
certo
volume, ou, mais precisamente,
para
a
variação
dessa
entropia
ao
mudar
o
volume,
mantendo
constante
a
energia.
Observa
ele
que
"essa
equação
mostra
que
a
entropia
da
radiação
monocromática
de
densidade
suficientemente
pequena
varia
com
o
volume
como
a
entropia
de
um
gás
ideal...”
Depois
vai
adiante,
para
calcular
a
entropia
pelo
método
de Boltzmann, concluindo que:
"Se
a
radiação
monocromática
de
frequência
v
e
energia
E
é
encerrada
em
um
volume
v
por
paredes
perfeitamente
refletoras,
então
a
probabilidade
(relativa)
de
que
a
qualquer
momento
toda
a
energia
de
radiação
seja
encontrada
no
volume
parcial
n
do
volume
n
0
é dada por
A partir daí, concluímos ainda que a
radiação monocromática de pequena densidade de
energia (dentro do campo de validade da fórmula de
radiação de Wien) comporta-se, em relações
termodinâmicas teóricas, como se consistisse de quanta
distintos de energia independentes de magnitude hv. *
*
Para
facilitar
ao
leitor
moderno,
usei
as
constantes
h
e
k.
Einstein
usa
B
=
h/k
e
RN
=
k
sendo
R
a
constante
dos
gases e N o número de Avogadro.
Einstein
leva
esse
resultado
muito
a
sério,
a
despeito
da
prova
esmagadora
de
todos
os
fenômenos
de
propagação
em
favor
de
uma
teoria
de
ondas para a luz, e diz o seguinte:
"Se
então,
na
medida
da
dependência
da
entropia
no
volume,
a
radiação
monocromática
de
densidade
suficientemente
pequena
se
comporta
como
um
meio
descontínuo
consistindo
de
quanta
de
energia
de
magnitude
hv,
é
razoável
indagar-se
se
as
leis
de
emissão
e
transformação
da
luz
são
constituídas
como
se
a
luz
fosse
composta
desses
mesmos
quanta
de
energia.”
Trataremos desse assunto no
próximo capítulo". (Einstein, Annalen der Physik, 19, 143,
(1904).)
No
capítulo
seguinte,
ele
trata
do
efeito
fotoelétrico
bem
como
de
análises
fotoquímicas
e
outras
ideias.
Tudo
isso
são
exemplos
que
confirmam
sua hipótese dos quanta de luz.
Foi
enorme
o
progresso
realizado
a
partir
das
ideias
de
Planck.
Planck
tinha
apenas
quantizado
os
osciladores
materiais
formando
as
paredes
do
corpo-negro,
talvez
sem
mesmo
acreditar
na
realidade
de
níveis
de
energia.
O
tônus
do
trabalho
inicial
de
Planck
—
e
mesmo
do
trabalho
posterior
—
dá
a
impressão
de
que
a
quantização
era
para
ele
pouco
mais
que
um
artificio
de
cálculo.
Para
Einstein,
por
outro
lado,
era
um
fenômeno
fundamental;
em
particular,
a
luz,
isto
é,
o
próprio
campo
eletromagnético,
é
quantizado.
Naturalmente
a
quantização
apresenta
enormes
dificuldades
se
se
tentar
conciliá-la
com
fenômenos
de
propagação
da
luz.
Em
vez
de
fugir
desses
problemas,
Einstein
reconheceu
sua
natureza
fundamental
e
nunca
deixou
de
meditar
sobre
eles
até
que
fossem
encontradas
as
soluções,
em
parte
por
ele
mesmo, em parte por outros físicos.
Agora
voltemo-nos
para
o
segundo
dos
estudos
de
Einstein
de
1905.
No
ano
de
1827,
o
botânico
escocês
Robert
Brown
(1773-1858)
observou
que
grãos
de
pólen
ou
outros
objetos
pequenos
suspensos
na
água
fazem
um
movimento
aleatório.
Esse
movimento,
chamado
de
browniano,
se
deve
ao
impacto
das
moléculas
do
fluido
que
cercam
o
objeto.
Einstein
apresenta
uma
teoria
sobre
o
movimento
browniano,
com
base
na
teoria
cinética
dos
gases.
Essa
teoria
dá
um
método
novo
e
direto
para
determinar
a
constante
de
Boltzmann
e,
por
conseguinte,
o
número
de
Avogadro,
e
uma
prova
quase
tangível
da
existência
de moléculas.
Esses
trabalhos
extraordinários
foram
notados
pela
comunidade
científica:
já
em
março
de
1906,
Planck
publicou
um
estudo
de
Einstein
sobre
a
teoria
da
relatividade.
Mas
ninguém
tinha
visto
o
autor.
Nem
o
autor
havia
deixado
o
escritório
de
patentes
para
conversar
com
os
grandes
físicos
teóricos.
Não
obstante,
alguns
jovens
e
ousados
cientistas
decidiram
ir
a
Berna
para
saber
quem
era
aquele
Senhor
Albert
Einstein.
Encontraram-no
em
seu
escritório.
Sua
vida
particular
parecia
um
tanto
boêmia,
mas
ele
era
polido
e
prontificou-se
a
esclarecer
quaisquer
dúvidas
que
existissem
a
respeito
de
suas
ideias.
Einstein
começou
a
corresponder-se
com
Planck
e
Lorentz
e
logo
as
autoridades
suíças
ofereceram-lhe
um
modesto
cargo
na
Universidade
de
Berna.
De
início,
não
quiseram
nomeá-lo
Privat
Dozent
por
questões
burocráticas,
mas
em
1908
a
Universidade
de
Zurique
concedeu-lhe
tal
título.
A
Universidade
Alemã
de
Praga
ofereceu-lhe
uma
cátedra
em
1909
e
ele
a
aceitou.
Mas
Einstein
não
se
sentia
feliz
em
Praga,
na
Áustria
dos
Habsburgos,
onde
predominava
uma
atmosfera
hipócrita
e
antissemita.
Einstein
não
tinha
muita
simpatia
pela
religião
em
termos
formais
e
era
fundamentalmente
agnóstico,
pelo
menos
no
que
diz
respeito
a
qualquer
teologia
formal.
Ficou
aliviado
quando,
em
1912,
pôde
retornar
à
sua
amada
Suíça,
desta
vez
para
a
Escola
Politécnica
de
Zurique, onde havia estudado.
Em
Praga,
Einstein
fizera
amizade
com
P.
Ehrenfest,
amizade
que
mais
tarde
veio
a
fortalecer-se
e
durou
até
a
morte
de
Ehrenfest.
Paul
Ehrenfest
(1880-1933)
era
um
físico
teórico
austríaco
que
tinha
sido
aluno
de
Boltzmann.
Casara-se
com
uma
física
russa,
Tatiana,
e
com
ela
escreveu
um
famoso
artigo
sobre
mecânica
estatística
para
a
Encyclopedia
of
Mathematics.
Ehrenfest
possuía
mais
capacidade
para
esclarecer
pontos
obscuros
da
física
do
que
para
criar
teorias
originais.
Era
um
professor
de
alta
capacidade
didática
e
demonstrava
muita
diligência
nas
tentativas
de
identificar
novos
talentos.
Era
famoso
pelo
afeto
com
quem
encorajava
os
jovens
e
estimado
e
estimado
por
seus
muitos
amigos
e
alunos,
em
razão
de
suas
qualidades
humanas.
Sucedeu
a
Lorentz
em
1912
e
fundou
uma
escola
que
logo
começou
a
ampliar-se.
Infelizmente,
Ehrenfest
era
sujeito
a
fases
de
profunda
depressão e, durante uma delas, em 1933, suicidou-se.
Um
estudante
de
físico-química
originário
de
rica
família
de
Praga
uniu-se
a
Einstein.
Tratava-se
de
Otto
Stern
(1888-1969).
Stern
havia-se
dado
conta
de
que
Einstein
era
o
físico
do
futuro,
ou
melhor,
do
presente,
e
aproveitou-se
de
sua
própria
independência
financeira
para
estudar
e
trabalhar
com
ele.
Este
é
outro
exemplo
do
inter-relacionamento
das
carreiras de muitos dos grandes físicos.
Por
essa
época,
Einstein
já
se
tinha
tornado
um
físico
importante
do
ponto
de
vista
profissional.
Em
1909,
em
uma
reunião
realizada
em
Salzburg,
conheceu
Planck,
Wien,
Sommerfeld,
Rubens,
Nernst
e
outros
grandes
físicos
modernos.
Sentiu
prazer
em
debater
frente
a
frente
com
todos
eles.
Antes
disso,
porém,
já
havia aperfeiçoado suas ideias de 1905.
Conforme
mencionei
acima,
ao
calcular
a
entropia
da
radiação
e
adotar
a
lei
de
Wien
para
u(v,T),
Einstein
concebera
a
ideia
dos
quanta
de
luz
e
relacionara-a
com
provas
experimentais.
A
entropia
da
radiação
está
intimamente
vinculada
à
flutuação
da
energia
contida
em
um
determinado
volume
e
a
hipótese
dos
quanta
de
luz
fornece
uma
expressão
bastante
simples
para
tais
flutuações.
O
que
acontece
se
se
efetuam
os
cálculos,
usando,
não
a
lei
aproximada
de
Wien,
que
só
é
válida
se
hV
>>>kT,
mas
a
lei
exata
de
Planck?
Einstein
fez
o
cálculo
mais
uma
vez
e
conseguiu
uma
fórmula
notável
para
a
flutuação
da
energia
contida
em
um
volume
fixo
e
em
certo
intervalo
de
frequência em torno de V.
Einstein
achou
dois
termos
que
tinham
de
ser
somados.
O
primeiro
é
um
termo
obtido
em
1905
com
a
fórmula
de
Wien
e
é
perfeitamente
análogo
à
expressão
da
flutuação
do
número
de
moléculas
gasosas
em
um
volume.
Indica
a
estrutura
granular
da
energia
radiante
e
confirma
que
E
=
nhV,
isto
é,
que
a
luz
se
comporta
como
se
fosse
composta
de
quanta
de
energia
E
=
h
V
.
A
segunda
expressão,
por
outro
lado,
é
exatamente
a
que
se
obteria
a
partir
da
teoria
eletromagnética
pura
e
é
causada
pela
interferência
construtiva
ou
destrutiva
das
ondas.
O
fato,
digno
de
nota,
da
presença
de
ambos,
indica
a
natureza
dual
da
luz
—
ondulatória
e
corpuscular.
As
ideias
de
Newton
e
de
Huygens,
que
pareciam
exclusivas
entre
si,
são
confirmadas. Conforme Einstein escreveu em 1909:
"É
inegável
que
existe
um
extenso
grupo
de
dados,
relacionados
à
radiação,
que
mostram
ter
a
luz
certas
propriedades
fundamentais
que
podem
ser
entendidas
muito
mais
facilmente
a
partir
do
ponto
de
vista
da
teoria
newtoniana
de
emissão
do
que
a
partir
do
ponto
de
vista
da
teoria
ondulatória.
Portanto,
sou
de
opinião
que
a
próxima
fase
do
desenvolvimento
da
física
teórica
nos
trará
uma
teoria
da
luz
que
pode
ser
interpretada
como
uma
espécie
de
fusão
das
teorias
ondulatória e da emissão..."
Enquanto
isso,
em
1907,
Einstein
havia
descoberto
outra
importante
aplicação
das
ideias
do
quantum.
Em
1819,
P.L.
Dulong
e
A.
T.
Petit
tinham
anunciado
que,
segundo
seus
cálculos,
"Les
atomes
de
tous
les
corps
simples
ont
exactement
Ia
même
capacité
pour
Ia
chaleur"
("Os
átomos
de
todos
os
elementos
têm
exatamente
a
mesma
capacidade
térmica"),
e
Boltzmann
tinha
explicado
esse
fato
com
o
princípio
da
equipartição
da
energia.
No
entanto,
quando
se
tornou
possível
medir
calores
específicos
a
baixas
temperaturas,
graças
à
disponibilidade
de
ar
líquido
e
a
outros
métodos
criogênicos,
descobriu-se
que
a
lei
de
Dulong
e
Petit
tinha
muitas
exceções.
Einstein
forneceu
a
razão
para
a
dependência
de
temperatura
do
calor
específico
representando
átomos
em
cristais
como
osciladores
de
determinada
frequência.
Segundo
a
teoria
dos
quanta,
eles
só
poderiam
ter
a
energia
nhv
com
n
como
número
inteiro.
Se
hv<<
kT,
estaremos
no
domínio
da
física
clássica
e
os
osciladores
terão
a
energia
média
de
3kT.
O
calor
atômico,
isto
é,
o
calor
específico
referente
a
um
átomo,
é
3k,
conforme
Dulong
e
Petit
haviam
achado.
Se,
entretanto,
kT
<<hv,
a
quantização
torna-se
apreciável
e
obteremos
um
calor
específico
muito
diferente
do
clássico.
Do
ponto
de
vista
qualitativo,
quando
os
osciladores
são
altamente
estimulados,
a
adição
de
um
quantum
de
energia
produz
uma
mudança
energética
que
é
pequena
em
comparação
à
energia
já
existente
no
oscilador
e
aí
não
estaremos
muito
longe
do
caso
clássico,
que
pressupõe
que
a
energia
muda
continuamente.
Para
que
tal
situação
ocorra,
a
temperatura
do
ambiente
em
volta
do
oscilador
deve
ser
tal,
que
kT
>>
hv.
Na
realidade,
a
energia
do
oscilador
será
então
kT
em
termos
brutos,
o
que
é
muito,
se
comparado
com
os
possíveis
saltos
de
energia
hV.
No
caso
extremo
e
oposto
kT
<<
hv,
a
agitação
da
temperatura
é
insuficiente
para
produzir
saltos
de
quanta
no
oscilador,
que,
assim,
se
torna
incapaz
de
absorver
energia
do
ambiente
em
torno.
O
comportamento
do
oscilador
é
dominado
por
suas
propriedades quânticas e o calor específico desaparece.
A teoria foi aperfeiçoada por P. Debye e
outros e está em consonância com dados
experimentais.
Tais
considerações
são
importantes
porque
mostram
que
a
constante
h
desempenha
um
papel
vital
na
mecânica
das
moléculas
e
dos
átomos.
O
êxito
desses
conceitos
serviu
para
despertar
mais
interesse
ainda
pelas
conceituações
quânticas,
que
ainda
se
restringiam a um círculo muito reduzido de iniciados.
Em
1911,
realizou-se
a
primeira
série
de
Conferências
Solvay
sobre
radiação
e
quanta.
Essas
conferências
derivam
seu
nome
de
Ernst
Solvay,
o
inventor
de
um
método
industrial
para
a
preparação
de
carbonato
de
sódio,
ou
soda.
Solvay
instituiu
e
financiou
uma
série
de
encontros
internacionais
sobre
física,
com
temas
preestabelecidos,
para
os
quais
se
convidavam
os
grandes
físicos
relacionados
à
área
escolhida.
As
conferências,
limitadas
a
cerca
de
trinta
pessoas,
tinham
lugar
em
Bruxelas.
A
orientação
dos
debates
e
a
relação
de
convidados
para
o
primeiro
deles
eram
elaboradas
em
grande
parte
por
H.
Walther
Nernst
1864-1941
professor
de
físico-química
em
Berlim,
um
dos
principais
termodinamicistas
da
época
e
uma
força
da
ciência
alemã.
Nernst
havia
descoberto
um
teorema
importante
às
vezes
chamado
de
terceiro
princípio
da
termodinâmica,
segundo
o
qual
a
entropia
de
qualquer
substância pura ao zero absoluto era a mesma: Zero.
Seu
teorema
tinha
profundas
raízes
na
teoria
quântica.
Em
razão
de
suas
altas
qualificações
em
física
e
linguística
e
de
suas
habilidades
diplomáticas
e
presságio
geral,
H.A.
Lorentz
era
um
convidado
permanente
e
quase
sempre
atuava
como
presidente
do
encontro.
O
número
restrito
de
participantes
e
o
nível
dos
convidados
asseguravam
debates
acalorados
e
profícuos.
Por
tradição,
os
soberanos
belgas
mostravam
seu
interesse
pelas
reuniões
convidando
os
participantes
a
um
jantar.
Como
resultado
desses
encontros,
Einstein
tomou-se
amigo
da
Rainha
Elizabeth
da
Bélgica
e
com
ela
manteve
uma
correspondência
que
durou muitos anos.
Na
conferência
de
1911,
Planck,
como
sempre,
manifestou
um
ponto
de
vista
conservador
e
prudente,
enquanto
Einstein,
que
estava-se
tornando
conhecido
como
a
figura
de
maior
realce,
mostrou-se
mais
flexível.
Pouco
depois,
quando
Einstein
recebeu
a
proposta
de
uma
cátedra
na
Escola
Politécnica
de
Zurique,
Marie
Curie
e
Poincaré,
que
o
haviam
conhecido
na
reunião
de
Solvay,
expressaram
abertamente,
em
uma
carta
de
recomendação,
o
alto
conceito que por ele tinham.
Einstein
foi
para
a
Escola
Politécnica
em
1912,
mas
ali
ficou
pouco
tempo.
Os
grandes
físicos
de
Berlim
o
queriam
na
capital
do
Reich
e
assim
apresentaram-lhe
ofertas
bastante
atrativas
para
o
Kaiser
Wilhelm
Institute
ou
para
a
Academia
Prussiana,
à
sua
livre
escolha.
As
funções
de
magistério
seriam
mínimas
e
ele
teria
a
máxima
liberdade
para
trabalhar,
um
salário
generoso
e
outras
vantagens.
Nernst
e
Planck
foram
a
Zurique
para
apresentar
a
oferta
pessoalmente,
o
que
constituiu
uma
atitude
rara.
Einstein
não
precisou
de
mais
que
um
dia
para
decidir-
se.
Informou
aos
visitantes
que
daria
um
passeio
e
retornaria
com
uma
rosa—
uma
rosa
vermelha
se
aceitasse
ou
uma
rosa
branca
se
recusasse.
Retornou
com
uma
rosa
vermelha.
Mas
insistiu
em
uma
condição:
queria
manter
a
cidadania
suíça.
Essa
insistência
provocou
alguns
problemas,
pois,
embora
Einstein
se
considerasse
cidadão
suíço,
a
Prússia
o
considerava
cidadão prussiano.
A
despeito
de
sua
brilhante
posição,
Einstein
não
se
sentia
bem
na
Alemanha
imperial.
Apreciava
a
companhia
dos
colegas
e
outras
atrações
oferecidas
por
Berlim,
mas
não
o
militarismo
prussiano.
Para
escapar
à
atmosfera
de
quartel
que
sentia
em
Berlim,
quase
sempre
ia
até
a
Holanda,
para
encontrar-
se
com
os
amigos
Lorentz
e
Ehrenfest.
No
início
de
sua
estada
na
Alemanha,
Einstein
divorciou-se;
mais
tarde,
veio
a
casar-se
com
uma
prima,
com
quem
viveu
o
resto
de sua vida.
Estamo-nos
aproximando
do
fatal
agosto
de
1914.
Einstein
estava
engajado
nas
primeiras
pesquisas
sobre
a
relatividade
geral,
uma
ampla
extensão
do
princípio
da
relatividade
para
movimentos
arbitrários.
É
claro
que
dois
sistemas,
acelerados
um
em
comparação
com
o
outro,
não
são
equivalentes.
O
fato
é
que
aparecem
forças
inerciais
em
um
que
não
são
encontradas
no
outro.
Um
exemplo
simples
é
um
elevador
em
queda
livre
sobre
a
superfície
da
terra:
para
um
observador
que
esteja
dentro
dele,
a
gravidade
desaparece.
Tal
fato
obviamente
não
é
a
mesma
coisa
que
um
elevador
em
repouso
em
relação
à
terra,
para
o
qual
a
gravidade
efetivamente
existe.
Einstein,
no
entanto,
observou
que,
ao
introduzirem-se
campos
gravitacionais
apropriados,
podem-se
tornar
os
dois
sistemas
acelerados
equivalentes
um
ao
outro.
Para
que
isso
seja
possível,
é
necessário
que
as
massas
inerciais
que
aparecem
na
equação
F
=
ma
sejam
iguais
à
massa
gravitacional
que
aparece
na
F
=
kmm'/r2.
Esse
fato,
digno
de
nota,
quase
sempre
expresso
quando
se
diz
ser
a
massa
gravitacional
igual
à
massa
inercial,
tinha
sido
descoberto
por
Galileu
em
suas
experiências
quase
lendárias
na
torre
inclinada
de
Pisa
e
confirmado
por
Newton,
que
cuidadosamente
constatou
que
pêndulos
do
mesmo
comprimento,
mas
de
materiais
diferentes,
têm
o
mesmo
período.
Com
maior
precisão,
o
Barão
R.
von
Eõtvõs
confirmou
esse
fato
na
Hungria,
em
1891,
e
precisão
ainda
maior
foi
conseguida
por
R.H.
Dicke
em
1936.
A
relatividade
geral,
em
oposição
à
relatividade
restrita,
não
estava
na
primeira
linha
do
interesse
dos
físicos,
e
Einstein
teve
de
enfrentar
sozinho
o
problema.
Do
ponto
de
vista
matemático,
a
teoria
geral
é
consideravelmente
mais
difícil
do
que
a
teoria
específica
da
relatividade
e
exige
o
uso
de
"análise
tensorial",
que,
na
época,
era
praticamente
desconhecida
dos
físicos.
O
próprio
Einstein
sentiu-se
impedido
pelas
dificuldades
matemáticas,
até
que
seu
amigo
Grossmann
lhe
apresentou
as
obras
de
B.
Riemann
e
B.
Christoffel
e,
mais
importante,
as
de
G.
Ricci-Curbastro
e
T.
Levi-Civita,
que
forneceram
os
necessários
instrumentos
matemáticos.
Einstein
pôde
então
operar
em
espaços
curvos
e
relacionar
os
efeitos
gravitacionais
à
curvatura
do
espaço
que,
por
sua
vez,
é
relacionada à presença de matéria ou energia.
Estou-me
antecipando
um
pouco.
A
declaração
de
guerra
em
1914
foi
acompanhada
de
uma
investida
geral
de
patriotismo
ingênuo
e
primário,
especialmente
na
Alemanha.
Reagindo
às
acusações
lançadas
pelos
Aliados,
talvez
às
vezes
exageradas,
contra
a
Alemanha,
principalmente
no
que
diz
respeito
à
invasão
da
Bélgica
neutra,
os
cientistas
alemães
responderam
com
um
manifesto
defensivo
em
que
cada
frase
começava
com
a
expressão:
"Es
ist
nicht
wahr.
..
(Não
é
verdade...)
e,
ao
final,
proclamava
a
solidariedade
dos
cientistas
com
os
militares.
Infelizmente,
entre
os
signatários
do
manifesto
estavam
nomes
altamente
respeitáveis,
como
Roentgen,
Planck,
Nernst,
Wien
e
muitos
outros.
Quando
se
dava
o
caso,
eles
acrescentavam
títulos
aos
nomes,
como
Geheimrat
(Conselheiro
Privado
do
Imperador)
ou
Excellenz
(Sua
Excelência),
detalhe
aliás
bastante
irônico,
se
pensarmos
que
alguém
como
Roentgen
poderia
imaginar
que
um
título
oficial
iria
acrescentar
força
à
sua
assinatura.
Mas
era
assim
a
Alemanha
imperial.
É
evidente
que
muitos
dos
signatários,
inclusive
Roentgen,
eram
ingênuos
e
mais
tarde
se
arrependeram
dessa
atitude.
Outros,
como
Planck,
aprenderam
a
lição
com
os
próprios
fatos.
Embora
continuassem
arraigadamente
patriotas,
não
foram
envolvidos
tempos
depois
pela
retórica
nacionalista
de
Hitler.
Einstein
recusou-se
a
assinar
o
documento
e
chegou
a
pensar
em
organizar
um
manifesto
de
oposição,
mas
não
levou
o
plano
adiante.
De
qualquer
modo,
já
havia
feito
sérios
inimigos
em
virtude de sua oposição política.
Einstein
estava
absorvido
em
seus
esforços
no
sentido
de
desenvolver
a
relatividade
geral.
Várias
vezes
julgou
ter
atingido
a
meta
tão
almejada,
logo
descobrindo
que
havia
falhas
graves
nessa
teoria.
Finalmente,
conseguiu
cumprir
seu
programa
de
formulação
de
leis
físicas
de
uma
maneira
válida
para
qualquer
sistema
de
referências,
provocando
uma
nova
interpretação
da
gravitação.
O
progresso
conceitual
e
a
clareza
da
teoria
são
marcantes,
embora
os
resultados
experimentais
sejam
modestos.
Previa
ela
alguns
pequenos
efeitos
que
podiam
fornecer
provas
experimentais:
a
mudança
do
periélio
de
Mercúrio;
o
desvio
de
raios
de
luz
por
uma
massa,
efeito
visível
em
um
eclipse
solar;
e
a
mudança
de
frequência
das
linhas
espectrais
emitidas
por
astros
maciços.
Infelizmente,
todos
esses
efeitos
são
pequenos
e
de
difícil
observação,
de
modo
que,
mesmo
agora,
não
há
nenhuma
confirmação
experimental
absoluta
ou
inequívoca
da
teoria
geral
da
relatividade.
Não
obstante,
a
redução
da
relatividade
a
um
efeito
geométrico
da
curvatura
do
espaço
é
um
conceito
magnífico
e
de
imensa
importância
em
astrofísica
e
cosmologia.
É
aqui
que
a
relatividade
geral
recebe
a
parte
que
lhe
cabe
e
se
torna
indispensável
para
descrever
e
interpretar
as
observações astronômicas.
Em
1917,
Einstein
publicou
outra
obra
de
grande
importância,
uma
nova
e
bem
simples
derivação
da
lei
do
corpo-negro,
que
dá
continuidade
a
conceitos
bastante
profundos.
A
emissão
de
luz
já
não
era
considerada
de
um
ponto
de
vista
maxwelliano.
Pela
primeira
vez,
leis
estatísticas,
as
mesmas
que
se
aplicam
ao
decaimento
radioativo,
eram
estendidas
a
fenômenos eletromagnéticos.
A
teoria
atômica
de
Bohr
já
existia
então,
mas
o
mecanismo
da
emissão
da
luz
a
partir
de
um
átomo
continuava
a
ser
um
mistério.
Einstein
conseguiu
levantar
uma
ponta
da
cortina
que
encobria
o
fenômeno
e
seus
documentos
de
1917
eram
muito
perspicazes
e
assinalaram
um
marco
na
teoria
moderna.
Neles,
abandonou
a
causalidade
estrita
da
física
clássica
e
apresentou
conceitos
de
probabilidade.
Nessas
condições,
seu
trabalho
continha
o
germe
da
mecânica
quântica
e
da
profunda
revolução
por
ela
causada.
Além
do
mais,
sem
qualquer
menção
explícita
das
aplicações,
continha
também
as
ideais
básicas
ao
funcionamento
dos
lasers
e
maser
tão
empregados
hoje
em dia.
Também
neste
caso
a
ideia
profunda
de
Einstein
é
tão
simples,
que
pode
ser
explicitada
em
palavras, sem ser necessário recorrer a fórmulas.
Einstein
examinou
um
corpo-negro
em
equilíbrio
térmico
contendo,
além
da
radiação,
átomos
especificamente
simples
com
apenas
dois
níveis
de
energia.
Um
pode
passar
de
um
nível
para
o
outro
emitindo
ou
absorvendo
um
quantum
de
luz
de
frequência
v
=
(E1
-
E2)h,
onde
E1
e
E2
são
as
energias
dos
dois
níveis.
Ao
precisar
que
o
átomo
e
a
radiação
se
mantêm
em
equilíbrio
estatístico,
isto
é,
que
o
número
de
átomos
que
passam
por
segundo
do
estágio
inferior
para
o
estágio
superior,
ou
vice-versa,
é
o
mesmo,
obteve
ele
notáveis
relações
entre
as
probabilidades
de
transição
e
a
emissividade
da
radiação.
Baseou
o
cálculo
na
probabilidade
de
ocorrência
do
decaimento
radioativo,
adequadamente
modificada.
Trata-se
de
um
enfoque
radicalmente
distinto
do
método
eletromagnético
clássico.
Einstein
chamou
de
A
a
taxa
de
transferência
espontânea
do
átomo
do
nível
superior
para
o
inferior,
e
de
B
a
taxa
de
transferência
do
estágio
superior
para
o
inferior,
ou
vice-versa,
sob
a
influência
da
radiação
de
emissividade
u
(v,
T).
Entre
outras
coisas,
mostrou
que
as
duas
taxas
de
transferência
induzida
são
iguais.
O
A
e
o
B
de
Einstein
atualmente
constituem
um conceito básico em física.
A
introdução
dos
coeficientes
A
e
B
com
seu
significado
baseado
na
probabilidade,
em
conexão
com
a
emissão
de
luz,
representa
uma
tendência
inteiramente
nova
e
um
prenúncio
de
coisas
que
estavam para acontecer.
Nesse
mesmo
documento
de
1917,
Einstein
forneceu
também
uma
nova
prova
do
resultado
que
havia
conseguido
anos
antes,
o
qual
dizia
que,
além
da
energia
hv,
os
quanta
de
luz
também
têm
uma
quantidade
de
movimento
hv/c
no
sentido
da
propagação
da
luz.
De
um
modo
notável,
chegara
ele
a
essa
conclusão,
que
deriva
diretamente
da
relatividade,
mediante
análises
sutis
—
e
até
certo
ponto
recônditas
—
das
flutuações
da
energia
e
da
densidade
do
momentum (quantidade de movimento).
Enquanto
Einstein
estava
absorvido
nesses
estudos,
a
guerra
havia
tomado
seu
curso,
terminando
em
1918
com
a
derrota
da
Alemanha
e
a
ruína
do
velho
regime
do
Kaiser,
sem
nenhuma
lamentação
por
parte
de
Einstein.
Após
um
período
revolucionário,
a
nova
República
de
Weimar
trouxe
para
a
Alemanha
grandes
esperanças
de
democratização.
Mas
o
governo
mostrava-se
extremamente
fraco,
era
solapado
por
dentro
e
por
fora
e
incapaz
de
governar
com
o
vigor
necessário.
Em
1919,
ocorreu
um
eclipse
total
do
sol,
que
possibilitou
a
constatação
de
algumas
das
consequências
da
relatividade
geral.
Realizaram-se
várias
expedições
com
esse
propósito
e
os
resultados,
embora
não
muito
claros,
favoreceram
as
teorias
de
Einstein.
Nesse
ponto
é
que
a
popularidade
de
Einstein
eclodiu.
Por
motivos
que
não
são
para
mim
muito
claros,
ele
repentinamente
se
tornou
uma
figura
bastante
popular,
mesmo
entre
pessoas
que
nada
conheciam
de
sua
obra.
Era
tratado
como
um
astro
de
cinema
ou
como
um
grande
animador
de
auditório,
mas
também
passou
a
ter
inimigos
figadais,
sem
qualquer
motivo
racional.
Surgiu
até
mesmo
uma
sociedade
científica
ante
einsteiniana,
onde
nomes
respeitados
e
respeitáveis
se
misturavam
a
demagogos,
dementes
e
futuros
recrutas
nazistas.
Einstein
era
convidado
a
fazer
palestras
em
público
sobre
a
relatividade.
Aceitava
tais
convites,
mas
as
palestras
eram
interrompidas
por
seus
adversários
e
transformadas
em
torpes
demonstrações
políticas.
Einstein
não
tinha
muito
autocontrole
e
reagia
através
da
imprensa
de
uma
maneira
que,
segundo
seus
amigos mais íntimos, não era absolutamente a ideal.
A
situação
tomou
um
rumo
difícil,
pois
os
extremistas
não
hesitavam
em
assassinar
os
inimigos.
O
assassinato
de
W.
Rathenau,
Ministro
dos
Negócios
Estrangeiros
da
República
de
Weimar,
foi
uma
advertência
a
respeito
do
que
poderia
acontecer.
Tratava-se
de
um
grande
patriota
e
figura
ilustre
da
indústria
alemã
que
trabalhara
infatigável
e
proveitosamente
em
favor
da
organização
da
economia
de
guerra
e
depois
fora
elevado
ao
cargo
de
Ministro.
Era
amigo
pessoal
de
Einstein
e
sua
morte,
bem
como
a
dos
socialistas
K.
Liebknecht
e
Rosa
Luxemburgo,
e
de
outras
figuras
notáveis,
era
apenas
o
prelúdio
do
que
viria a acontecer durante a era nazista.
Einstein
já
estava
se
sentindo
saturado
e
iniciou
uma
longa
viagem
pelo
mundo.
Os
amigos
Planck,
von
Laue
e
outros,
insistiam
em
que
ele
não
deveria
abandonar
a
Alemanha
num
período
difícil
como
aquele
e
em
que
não
deveria
aceitar
nenhuma
das
inúmeras
propostas
que
vinha
recebendo
do
exterior.
Leyden
atraía-o
de
maneira
bastante
peculiar
tanto
por
causa
de
sua
amizade
com
Ehrenfest
quanto
por
causa
da
insistência
de
Lorentz
em
que
ele
ali
se
fixasse.
Mas,
ao
final
da
viagem,
Einstein
voltou
a
Berlim
depois
de
ter
estabelecido
relações
pessoais
nos
Estados
Unidos
e
em
outros
países.
A
situação
parecia
ter-se
acalmado
um
pouco
por
volta
de
1924,
e
ele
passou
a
levar
uma
vida
social
relativamente
ativa.
Em
casa,
recebia
grande
variedade
de
pessoas,
inclusive
o
pintor
Sleevogt,
o
médico
Plesch,
o
químico
P.
Haber,
os
músicos
F.
Kresiler
e
A.
Schnabel,
o
industrial
e
Ministro
do
Exterior
Graf
Rantzrau
e
o
pintor
M.
Liebermann.
Em
seus
momentos
de
lazer,
continuava
a
tocar
violino,
atividade
que
exerceu
durante
toda
a
vida.
Não
se
opunha
a
representar
o
papel
do
grande
cientista
e
era
evidente
que
gostava
disso.
Talvez
esse
fato
explique
algumas
de
suas
afetações,
sua
estranha
maneira
de
vestir-se
e
alguns
hábitos
que
podem
ter
sido
um
tanto
exibicionistas.
Afinal
de
contas,
era
admirador
e
amigo
de Charlie Chaplin.
Mas
nenhuma
dessas
atividades
desviava
Einstein
de
seus
estudos
mais
sérios.
O
ano
de
1922
fora
testemunha
de
outra
confirmação
espetacular
de
seus
conceitos
sobre
os
quanta,
quando
o
físico
norte-
americano
Arthur
Holly
Compton
(1892-1967)
descobriu
que
os
Raios
-
X
eram
difundidos
por
elétrons
livres
como
partículas
com
uma
energia
hv
e
com
um
momentum
hv/c,
conforme
Einstein
havia
predito.
Particularmente,
o
quantum
difundido
tinha
uma
frequência
diferente,
que
variava
de
acordo
com
o
angulo
de
difusão.
Eram
fatos
que
a
teoria
ondulatória
não poderia explicar.
A
dualidade
onda-corpúsculo
da
luz
estava-
se
tornando
cada
vez
mais
evidente,
quando
um
físico
indiano
desconhecido,
Satiendranath
(S.N.)
Bose
(1894-
1974),
apresentou
um
manuscrito
a
Einstein
em
busca
de
sua
opinião.
O
manuscrito
continha
uma
nova
confirmação
da
fórmula
do
corpo-negro,
obtida
através
da
mecânica
estatística;
mas
Bose
considerava
quanta
de
luz,
aos
quais
aplicava
a
mecânica
estatística,
de
uma
forma
diferente
da
usual.
A
diferença
básica
é
que,
na
mecânica
estatística
de
Boltzmann,
cada
molécula
tem
uma
individualidade;
portanto,
podemos
designar
cada
uma
por
um
nome
e
assim
reconhecê-la.
Em
contraste,
para
Bose,
os
quanta
de
luz
são
absolutamente
idênticos.
Para
Boltzmann
a
troca
da
molécula
A
pela
molécula
B
permite
uma
nova
configuração,
que
deve
ser
considerada
à
parte;
mas
para
Bose
a
troca
de
dois
quanta
idênticos
não
implica
outra
configuração.
O
resultado
é
uma
nova
confirmação
da
fórmula
do
corpo-
negro.
Einstein
leu
o
trabalho
que
Bose
lhe
havia
enviado,
traduziu-o
e
fez
com
que
fosse
publicado
em
um
periódico
alemão,
acrescentando
algumas
palavras
de
louvor
e
o
comentário
de
que
o
que
Bose
tinha
feito
pelos
quanta
de
luz
ele
mesmo,
Einstein,
demonstraria
ser
também
possível
para
as
moléculas.
Einstein
manteve
a
promessa
e
em
1924
publicou
um
trabalho
sobre
o
tema.
Assim
surgiram
as
novas
estatísticas,
que
seriam
complementadas
dois
anos
depois
pela
obra
de
Fermi
e
Dirac,
que
mostraram
não
serem
as
estatísticas
de
Bose
e
de
Einstein
as
únicas
possíveis,
mas
que,
na
natureza,
existem
os
dois
tipos.
Trataremos
dessa
questão mais adiante, quando falarmos de Fermi.
Como
era
de
se
esperar,
Einstein
também
calculou
as
flutuações
de
um
gás
Bose-Einstein
e
mais
uma
vez
descobriu
um
indício
da
natureza
dual
não
apenas
dos
quanta,
mas
também
—
e
aí
vinha
uma
novidade — das moléculas.
A
dualidade
onda-corpúsculo
estava-se
tornando
cada
vez
mais
evidente
a
partir
da
nuvem
de
mistério
em
que
estava
envolvida.
Mais
ou
menos
naquela
época,
L.
de
Broglie
fez
progressos
decisivos
nesse
campo,
mas
aqui
também
a
contribuição
de
Einstein
foi
muito
importante,
sobretudo
em
seu
papel
de avalista de conceitos novos e surpreendentes.
À
proporção
que
a
fama
de
Einstein
crescia,
ele
ia
fazendo
pronunciamentos
políticos
e
humanitários
com
maior
frequência.
Também
assumiu
uma
posição
firme
de
pacifista
e
de
defensor
do
Estado
de
Israel.
Quando
Israel
foi
criado,
muitos
anos
mais
tarde,
ofereceram
a
Einstein
o
cargo
de
Presidente,
mas,
sabendo
de
suas
próprias
qualidades
e
limitações,
ele
declinou
do
convite.
Qualquer
boa
causa
podia
ganhar
o
apoio
de
Einstein,
do
mesmo
modo
como
qualquer
bom
físico
que
ele
conhecesse
poderia
obter
uma
recomendação
de
sua
parte.
Assim,
ironicamente,
qualquer
recomendação
feita
por
Einstein,
que
prima
facie deveria significar muito, passou a não ter valor.
Em
1927,
a
mecânica
quântica
não-
relativista
já
poderia
ser
considerada
completa
e
as
primeiras
linhas
de
sua
interpretação,
segundo
a
famosa
interpretação
de
Copenhague,
já
haviam
sido
formuladas.
Bohr
apresentou
um
documento
a
esse
respeito
à
Conferência
Internacional
de
Física,
realizada
em
Como
para
celebrar
o
centenário
de
Volta.
Einstein
não
compareceu
à
Conferência
porque
não
queria
visitar
a
Itália
fascista,
mas
pouco
mais
tarde,
quando
Bohr
repetiu
as
mesmas
ideias
no
Conselho
Solvay,
recebeu
a
oposição
de
Einstein.
Bohr,
que
muitas
vezes
se
inspirara
em
Einstein,
tinha
por
ele
verdadeira
idolatria,
e
Einstein
já
fizera
repetidas
manifestações
de
admiração
e
apreço
por
seu
colega.
A
rejeição
de
Einstein
aos
mais
caros
conceitos
de
Bohr
deixaram-no
amargurado
e
desorientado.
Surgiu
daí
um
longo
debate,
durante
o
qual
Bohr
destruiu
todas
as
objeções
apresentadas
por
Einstein,
mas
teve
de
enfrentar
outras,
sem,
contudo,
conseguir
convencê-lo.
Até
o
fim
da
vida,
Einstein,
um
dos
grandes
criadores
da
física
quântica,
manteve-se
cético
quanto
à
interpretação
de
Copenhague,
embora
estivesse
ficando
cada
vez
mais
isolado em seu ponto de vista.
Com
a
ascensão
do
nazismo,
Einstein
finalmente
emigrou
da
Alemanha,
onde
sem
dúvida
alguma
teria
sido
morto,
e,
depois
de
alguma
peregrinação,
fixou-se
no
Instituto
de
Estudos
Avançados
de
Princeton,
New
Jersey.
A
chama
de
seu
gênio
estava-se
enfraquecendo
e
Einstein,
que
durante
décadas
enxergara
mais
à
frente
do
que
qualquer
outro
homem
e
introduzira
algumas
das
mais
profundas
e
mais
profícuas
ideias
no
campo
da
física,
passou
a
dedicar-se
a
problemas
que
aparentemente
não
tinham
solução
e
que
talvez
estivessem
sendo
colocados
de
forma
errônea.
As
linhas
mestras
da
nova
física
que
se
originaram
em
Berna
Zurique
e
Berlim
não
tiveram
sequência a partir de Princeton.
Não
obstante,
Einstein
ainda
estava
destinado
a
desempenhar
um
papel
importante,
embora
paradoxal
para
um
pacifista:
pressionar
os
Estados
Unidos
para
que
fosse
construída
a
bomba
atômica.
Chamo
esse
papel
de
paradoxal,
mas
trata-se
de
posição
que
se
enquadrava
em
seus
próprios
princípios
nas
circunstâncias
da
Segunda
Guerra
Mundial.
Mas
era
um
passo
mais
político
do
que
técnico:
Einstein
certamente
não
estava
em
dia
com
a
física
nuclear
da
década
de
quarenta,
nem
contribuiu
tecnicamente
para
o
desenvolvimento
da
energia
atômica.
Em
18
de
abril
de
1955,
terminou
seus
dias
tranquilamente,
em
Princeton,
aos
setenta
e
seis
anos
de idade.
A
respeito
de
si
próprio,
certa
vez
afirmou
o
seguinte:
"Deus
é
inexorável
no
oferecimento
de
dons.
Deu-me
apenas
a
teimosia
de
uma
mula.
Não!
Deu-me
também um agudo sentido de odor!"
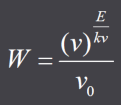
EMÍLIO
GINO
SEGRÉ
nasceu
em
Tivoli,
Itália
em
1905.
Em
1959
ganhou
o
Prêmio
Nobel
de
Física
com
a
descoberta
do
antipróton.
Já
lecionou
nas
principais
universidades
dos
Estados
Unidos.
Suas
pesquisas
e
seus
trabalhos
mais
importantes
sempre
se
voltaram
para
a
antimatéria.
Neste
artigo
Segré
mostra
que
a
lógica
de
Einstein
é
irrefutável,
embora
na
época
dele
soasse
desagradável
para
muitos
físicos,
em
razão
de
sua
aparente
contradição
com
a
experiência
do
cotidiano.
Segré,
na
década
de
60,
contribuiu
com
muitos
artigos
de
Física para a Enciclopédia Britânica.
Este
artigo
é
da
Revista
Humanidades
-
Universidade de Brasília
Julho/setembro 1983 - número 4




Cartas de Einstein ao Presidente Roosevelt - 1939
Carta de Einstein a Born - 1926
Carta de Einstein a Born - 1944
O princípio da Incerteza de Heisenberg - Henrique Fleming
Ciência e Weltanschauung - a Álgebra como Ciência Árabe - L. Jean Lauand
A contribuição de Einstein à Física - Giorgio Moscati
Antes de Newton Maria Stokes - AIP
Einstein: Novas formas de pensar Emílio Gino Segré
Símbolo e Realidade - Max Born
Um passeio pelas interações fundamentais na natureza Maria Stokes - AIP
Um Caminhada Através do Tempo
Episódio 1: Eunice Foote
Podcast episódio 1: Eunice Foote
Episódio 2: Arrhenius, Callendar e Keeling
Podcast episódio 2: Arrhenius, Callendar e Keeling
Episódio 3: Ciência das Mudanças Climáticas na década de 1970
Podcast episódio 3:Ciência das Mudanças Climáticas na década de 1970
Episódio 4: Contracultura Quântica
Podcast episódio 4: Contracultura Quântica
Episódio 5: Einstein estava errado?
Podcast episódio 5: Einstein estava errado?
Episódio 7: A presença afro-americana na física
Podcast episódio 7: A presença afro-americana na física
Episódio 8: Uma entrevista com o Dr. Ronald Mickens
Podcast episódio 8: Uma entrevista com o Dr. Ronald Mickens
Episódio 9: O Inesperado Herói da Luz
Podcast episódio 9: O Inesperado Herói da Luz
Episódio 10: O Newton que você não conhecia
Podcast episódio 10: O Newton que você não conhecia
Episódio 11: O Legado do Almagesto de Ptolomeu
Podcast episódio 11: O Legado do Almagesto de Ptolomeu

EINSTEIN: NOVAS FORMAS DE PENSAR
Se
Rafael
pudesse
voltar
à
vida,
certamente
pintaria
uma
moderna
Escola
de
Atenas
de
físicos.
E
naturalmente
incluiria
Einstein
junto
com
Galileu,
Newton
e
Maxwell
apontando
para
o
céu,
enquanto
Faraday
e
Rutherford
apontariam
para
a
terra.
Emílio Gino Segré














